Klimatický model dynamické jeskyně

Climatic Model of a Dynamic Cave

Antonín Jančařík

(Český kras 3; str.38—50; Beroun 1978)

 

---

Abstract

Für den Rechner WANG 2200 wurde ein Programm auf Grund der Beziehungen 1, 5, 6, 7 und 8 für die thermische Wetterführung in dynamisch ventilierten Höhlen aufgestellt. Die berechneten Ergebnisse stimmen mit den gemessenen ziemlich überein (Fig.2, 3). Mit dem beschriebenen Programm wurde eine Abschätzung der klimatischen Bedingungen vor der Öffnung der Koněprusy-Höhlen als Schauhöhlen berechnet.

 

0. Úvod

Mikroklimatologie jeskynních prostor (tzv. speleoklimatologie) má v současné době tyto základní úkoly:

• a) navrhovat vhodné úpravy, které by omezily nepříznivý vliv zásahu člověka do mikroklimatu jeskyně, především zpřístupněných,
• b) odhadem paleoklimatu jeskyní pomáhat při studiu podmínek vývoje krasové výzdoby,
• c) posuzovat vhodnost vybraných prostor pro speleoterapii.

Zvládnutí těchto úkolů vyžaduje studium všech vlivů, které jeskynní klima ovlivňují, tedy přechod od popisné klimatologie jakožto discipliny geografické ku klimatologii jakožto disciplině fyzikální.

Z klimatologického hlediska jsou jeskyně děleny do dvou základních skupin (KUNSKÝ 1950):

• a) dynamické jeskyně, ve kterých je rozdílný směr proudění v letním a v zimním období. Jeskyně tohoto typu mají dva nebo více vchodů s různou nadmořskou výškou, které jsou podle ročního období vtažné nebo výdušné.
• b) statické jeskyně, ve kterých alespoň vjedné polovině roku není výrazně převládající proudění. Jeskyně tohoto typu mají většinou pouze jeden vchod, od kterého buď stoupají nebo klesají. Do této skupiny patří většina propastí.

Ve skutečnosti se velmi často vyskytují jeskyně, jejichž jedna část je dynamická a druhá část statická.

Podle příčin, které proudění v jeskyních vyvolávají, je možné ho rozdělit do tří skupin:

• a) proudění termické – vyvolávané rozdílem tlaku vzduchových sloupců o rozdílných teplotách;
• b) proudění barické – vyvolávané změnami tlaku vzduchu ve vnější atmosféře;
• c) proudění vyvolané prouděním vzduchu na povrchu.

Zanedbána jsou proudění způsobená speciálními příčinami, např. oteplováním vzduchu od teplých minerálních pramenů v jeskyních (PICIOCCHI a UTILI 1975).

Aby bylo možno postihnout zákonitosti tvorby jeskynního klimatu, byly vypracovány matematické modely barického a termického proudění. Vzhledem k tomu, že proudění vyvolané prouděním na povrchu se výrazněji uplatňuje pouze v některých speciálních případech a model barického proudění byl popsán dříve (JANČAŘÍK 1977), bude v tomto příspěvku věnována pozornost pouze modelu termického proudění.

 

1. Modelování termického proudění

Pro modelování termického proudění bylo v prvém přiblížení použito následujících předpokladů:

• jde o jednoduchou chodbu s dvěma vchody (obr.1);
• proudění je vyvoláváno pouze rozdílem tlaků vzduchových sloupců o rozdílných teplotách;
• je zanedbán vliv vlhkosti;
• koeficient přestupu tepla je v celé jeskyni konstantní;
• povrchová teplota stěn není ovlivňována proudícím vzduchem;
• teplotní pole v profilech příčných na směr proudění je homogenní.

 

 

Obr.1: Idealizovaný tvar dynamické jeskyně.

Fig.1: Idealized shape of a dynamically ventilated cave.

 

 

Zanedbání vlhkosti nemá tak výrazný vliv, jak by se mohlo na první pohled zdát, protože je užíván koeficient přestupu zjevného tepla, tj. koeficient přestupu tepla bez uvažování změn celkové entalpie vlhkého vzduchu (JANČAŘÍK 1976b).

Změny tlaku s výškou se v praxi nejčastěji vypočítávají podle některého z následujících vzorců (JANČAŘÍK 1976a):

 

/1/

 

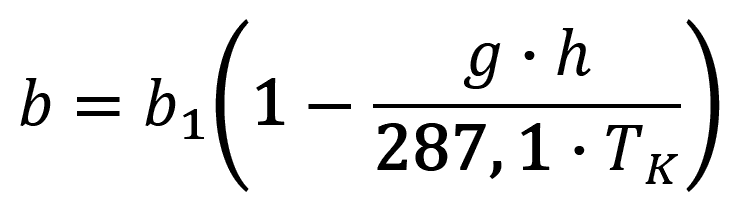
/2/

 

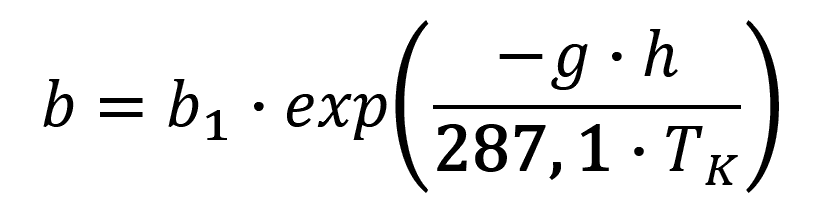
/3/

 

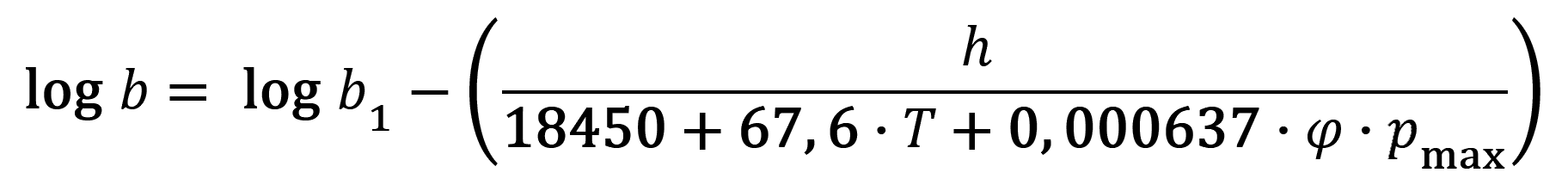
/4/

 

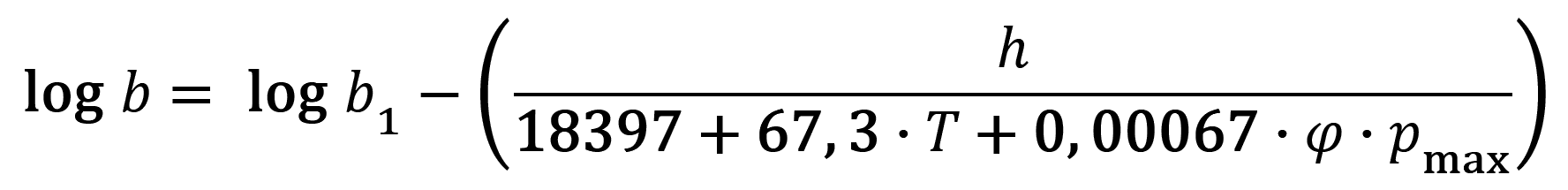
kde:

• b ... barický tlak v daném bodě  [Pa],
• b₁ ... barický tlak ve výchozím bodě  [Pa],
• h ... rozdíl geodetických výšek výchozího a daného bodu  [m],
• T ... střední teplota vzduchového sloupce  [°C],
• T_K ... střední teplota vzduchového sloupce  [°K],
• φ ... střední relativní vlhkost vzduchového sloupce  [%],
• p_max ... tlak nasycených par vody při teplotě T  [Pa].

Volba vhodného vzorce je závislá na požadované přesnosti. Na základě kontrolního propočtu byl zvolen vztah /1/.

Tlakový rozdíl vyvolaný rozdílem teploty volné atmosféry a střední teploty vertikálních úseků jeskyně uvádí její ovzduší do pohybu. Proti tomuto pohybu působí síly tření. Tento vliv je možno nejlépe vyjádřit tzv. aerodynamickým odporem:

 

/5/

 

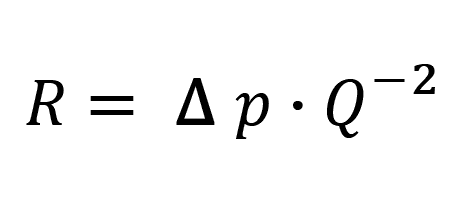
kde:

• R ... aerodynamický odpor mezi body A a B,
• Δp ... rozdíl tlaku mezi body A a B,
• Q ... průtočné objemové množství vzduchu mezi body A a B.

Zanedbáme-li vliv změn viskozity vzduchu, je možno aerodynamický odpor pro každou prostoru považovat za konstantní. Známe-li tedy tlakový rozdíl /1/ a aerodynamický odpor jeskyně, můžeme vypočítat /5/ průtočné množství vzduchu.

Pro výpočet teploty vzduchu v jeskyni bylo použito vzorce:

 

/6/

 

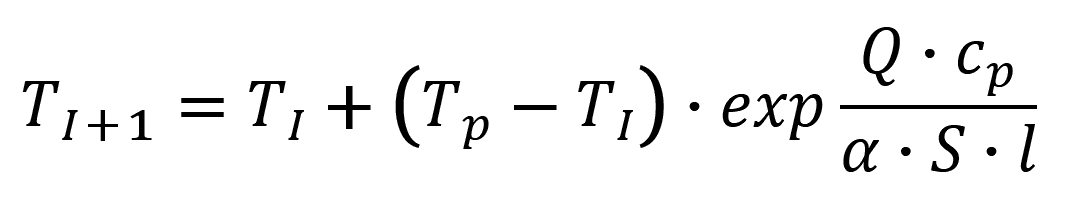
kde:

• T_I ... teplota vzduchu na začátku úseku,
• T_I+1 ... teplota vzduchu na konci úseku,
• T_p ... teplota horniny (povrchová),
• Q ... průtočné množství vzduchu,
• α ... alfa, koeficient přestupu tepla,
• S ... obvod chodby,
• l ... délka úseku,
• c_p ... měrné teplo vzduchu při stálém tlaku.

Přičemž teplota horniny byla vypočítávána ze vzorce:

 

/7/

 

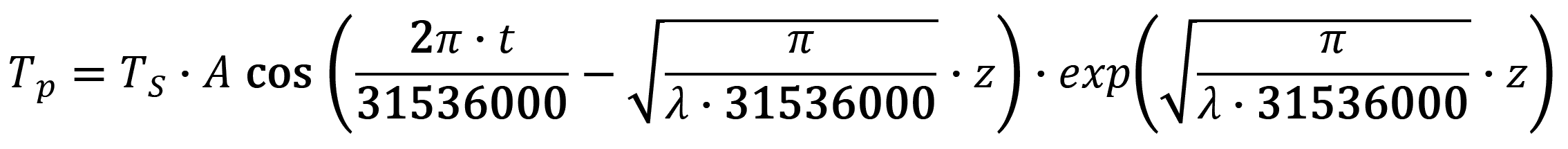
kde:

• T_s ... střední teplota vzduchu na povrchu,
• A ... amplituda teploty,
• z ... hloubka,
• λ ... tepelná vodivost horniny.

Na základě těchto vztahů byl vypracován výpočetní program pro kalkulátor WANG 2200.

Výpočet byl prováděn s velikostí délkových úseků 10⁰—10¹ m a s velikostí časových kroků 10⁴—10⁵ sec. Jako počáteční podmínka bylo položeno T_uvnitř = T_vně. Teplota vnějšího ovzduší byla interpolována z výsledků měření v Koněpruských jeskyních v letech 1970—1971 (LYSENKO 1975, 1976). Vzhledem k nízké rychlosti použitého kalkulátoru nebylo možno provést v každém časovém kroku iteraci průtočného množství vzhledem k teplotám uvnitř jeskyně. Proto byl zaveden předpoklad o malých změnách průtočného množství mezi jednotlivými kroky a při výpočtu teploty uvnitř jeskyně bylo používáno průtočné množství vypočtené z teplot předchozích.

Při výpočtu byly parametry jeskyně voleny podle zjednodušeného větrního schématu Koněpruských jeskyní.

Model postihuje základní vlastnosti jeskynního klimatu (utlumení teplotních kmitů), nepřirozeně výrazně se však projevuje vliv teploty horniny. Proto byla provedena úprava programu, která umožňuje zahrnout vliv proudícího vzduchu na povrchovou teplotu stěn. Vzhledem k tomu, že řešení rovnice vedení tepla v hornině s okrajovou podmínkou třetího druhu přesahuje rámec možností použitého kalkulátoru, byla zavedena korekce povrchové teploty podle vzorce (CARSLAW a JAEGER):

 

/8/

 

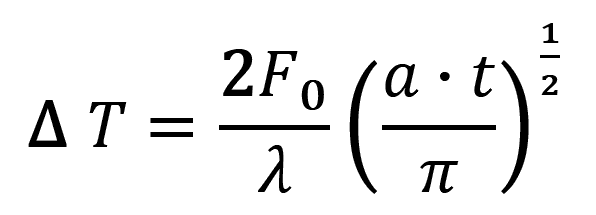
kde:

• ΔT ... změna povrchové teploty,
• F₀ ... tepelný tok,
• λ ... koeficient tepelné vodivosti horniny,
• a ... koeficient teplotní vodivosti horniny.

Tento vzorec byl sice odvozen za předpokladu, že v čase t = 0 je v hornině homogenní teplotní pole, avšak chyby, které vzniknou jeho zanedbáním, neovlivňují v našem případě výrazně přesnost výpočtu. Není možno však již zanedbat vliv vlhkosti, neboť změny latentního tepla bývají při průchodu vzduchu jeskyněmi výraznější než změny tepla zjevného (JANČAŘÍK 1976b). Proto byl zaveden zjednodušující předpoklad, že poměr změn latentního a zjevného tepla je při průchodu vzduchu jeskyněmi konstantní. Na základě měření v řadě jeskyní bylo dále stanoveno, že vzduch se nasytí vlhkostí v okamžiku, kdy dosáhne přibližně střední teploty na zemském povrchu (JANČAŘÍK 1976, LYSENKO 1976, KORDOS 1970, 1972).

Na základě vztahů:

 

/9/

 

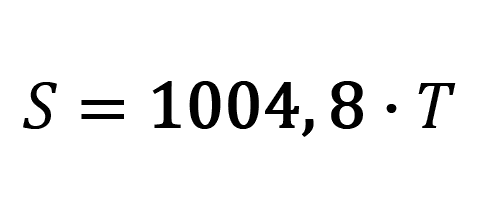
/10/

 

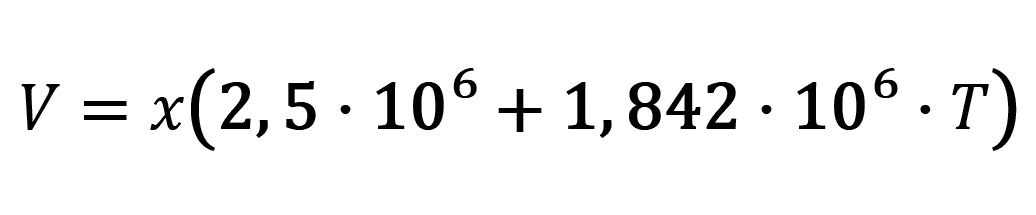
/11/

 

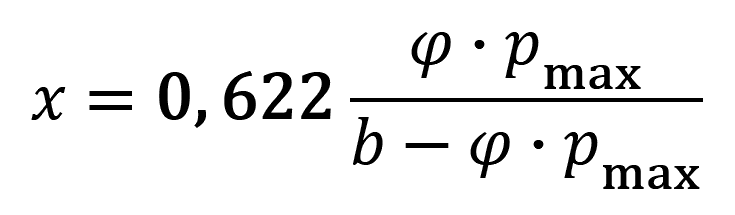
/12/

 

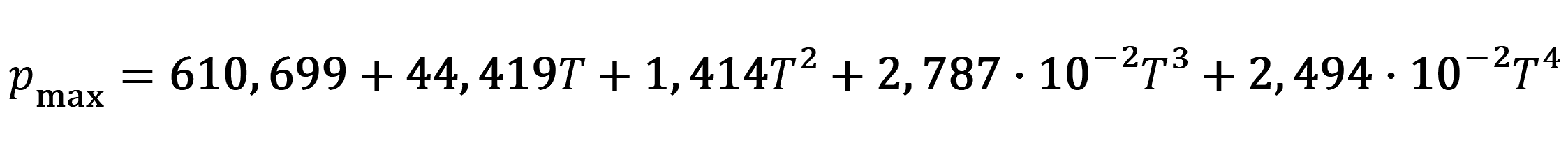
kde:

• S ... entalpie suchého vzduchu,
• V ... latentní teplo vzduchu,
• x ... vodní obsah vzduchu.

je pro okamžitý stav vnější atmosféry vypočítáván poměr:

 

/13/

 

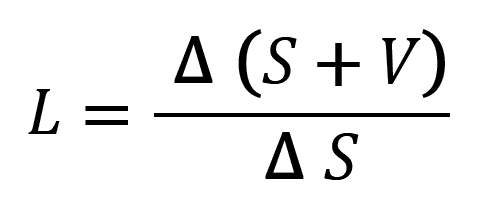
kterým násobený tepelný tok:

 

/14/

 

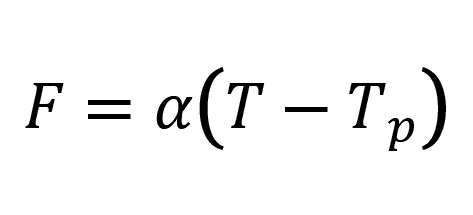
se dosazuje do vztahu /8/.

Na základě těchto předpokladů byl sestaven výpočetní program. Nízká rychlost použitého kalkulátoru neumožňuje použít iteračního procesu pro určení korekce povrchové teploty stěny, a proto byl použit předpoklad o malých změnách teploty ovzduší mezi jednotlivými časovými kroky a k výpočtu korekce je užívána teplota ovzduší z předešlého kroku. Velikost časových i délkových kroků a počáteční i okrajové podmínky jsou voleny stejně jako v předchozím případě.

Výsledky jednoho výpočtu spolu s teplotami skutečně naměřenými jsou uvedeny na obr.2.

 

 

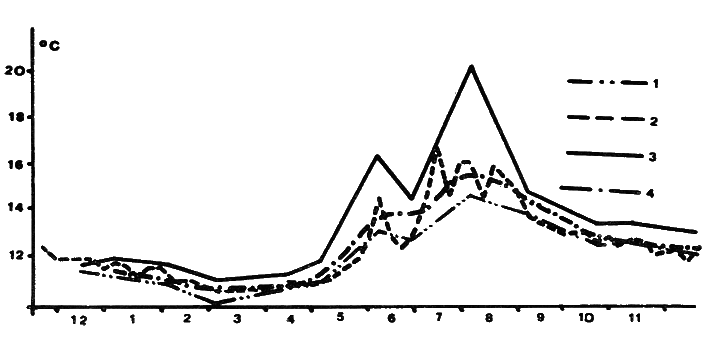
Obr.2: Roční chod teplot v Mincovně (Koněpruské jeskyně): 1 – u podlahy; 2 – ve středu prostory; 3 – u stropu; 4 – vypočtený.

Fig.2: Annual temperature variation in „Mincovna“ (Koněprusy Caves): 1 – at the floor; 2 – in the middle of the room; 3 – at the roof; 4 – calculated.

 

 

Srovnáme-li roční chod teploty vypočtený a skutečně naměřený, zjistíme, že výsledky výpočtu dobře odpovídají skutečnosti. Drobné úchylky mohou být způsobeny jednak vlivem neuvažovaných způsobů větrání, jednak zavedenými zjednodušujícími předpoklady. Z těchto má pravděpodobně největší význam předpoklad o homogenitě teplotního pole v příčných profilech. Ve skutečnosti existuje v některých částech jeskyní, a to především v blízkosti jejich vchodů, výrazný teplotní gradient (JANČAŘÍK 1976b, LYSENKO 1975, 1976, KORDOS 1970, 1972), který může v části profilu ukloněné chodby vyvolat proudění opačného směru než má proudění základní.

 

 

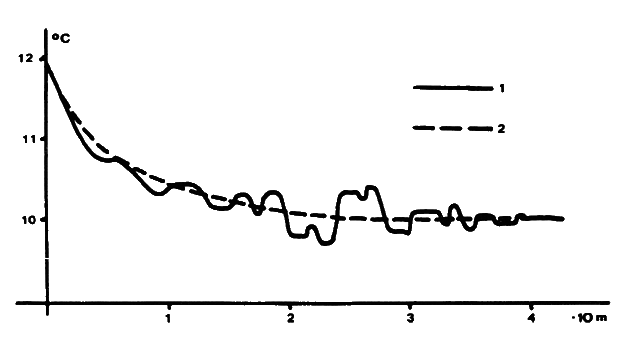
Obr.3: Závislost teploty na vzdálenosti od vchodu: 1 – naměřená; 2 – vypočtená.

Fig.3: Change of temperature with distance from the entrance: 1 – measured; 2 – calculated.

 

 

Porovnáme-li průběh teplot v závislosti na vzdálenosti od vchodu s výsledky některých měření (KORDOS 1970 – obr.3), vykazují výsledky poměrně dobrou shodu se skutečností s výjimkou oblasti vzdálenosti 20—30 m od vchodu. Jde o tzv. druhou Kordosovu zónu (KORDOS 1970, 1972), ve které dochází k vývinu turbulence v důsledku přestupu tepla a vlhkosti mezi ovzduším a horninou. Srovnáním s výsledky měření toku entalpie (JANČAŘÍK 1976b), prováděnými v blízkosti vchodu, zjistíme, že v této zóně dochází ke zvýšení poměru změn latentního a zjevného tepla. Toto zvýšení se s dalším postupem proudu vyrovnává. Je tedy možno předpokládat, že zavedení konstantního poměru latentního a zjevného tepla může v některých oblastech ovlivnit přesnost výpočtu. Přes uvedené nedostatky je možno tímto způsobem modelovat s uspokojivými výsledky termické proudění v jeskyních.

 

2. Odhad mikroklimatu Koněpruských jeskyní před provedením zpřístupňovacích prací

Zpřístupněním Koněpruských jeskyní došlo k výrazné změně jejich mikroklimatu, což se již v některých případech nepříznivě projevilo na výzdobě. Podle předpisů ČBÚ (1977) se má větrání zpřístupněných jeskyní organizovat tak, aby pokud možno nebylo narušeno jejich původní mikroklima.

Bohužel bylo v období před zpřístupněním v Koněpruských jeskyních provedeno pouze několik náhodných měření. Proto byl proveden pokus o odhad klimatických podmínek před zpřístupněním pomocí modelu termického proudění.

Základními předpoklady jsou, že před zpřístupněním byly větrně odděleny východní části středních pater, Proškův dóm a spodní patra a že aerodynamický odpor byl asi pětkrát větší než v současné době. Na základě těchto předpokladů byl proveden výpočet, jehož výsledky jsou uvedeny na obr.4. Porovnáním s obr.2 zjistíme výrazné změny v ročním chodu teploty. V současné době, kdy se pravidelně uzavírají vstupní dvéře do Mincovny, přiblížil se roční chod poněkud situaci před zpřístupněním, avšak výrazné zlepšení přinese teprve dlouho připravované zabudování druhých dveří ve vstupní chodbě tak, aby byly neustále alespoň jedny dveře z dvojice zavřeny.

 

 

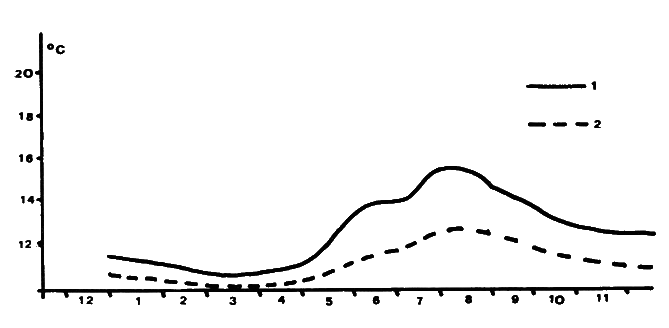
Obr.4: Změna mikroklimatu v Mincovně (Koněpruské jeskyně): 1 – střední teplota po zpřístupnění; 2 – střední teplota před zpřístupněním (vypočtená).

Fig.4: Change of climate in „Mincovna“ (Koněprusy Caves): 1 – mean temperature after opening for public; 2 – mean temperature before opening for public (calculated).

 

 

3. Závěr

Uvedené způsoby modelování základních způsobů proudění, i když jsou výrazně omezeny možnostmi použitého kalkulátoru, umožňují dobře postihnout jejich vlastnosti. Přestože jedním ze základních předpokladů uvedených modelů je jednoduchý tvar jeskyně, je možno je používat v některých případech i v daleko složitějších systémech. Rozpracování modelů tak, aby byl odstraněn tento zjednodušující předpoklad, je realizovatelné pouze na výrazně výkonnějším počítači. Stejná je situace i u dalších zjednodušujících předpokladů, zejména při řešení rovnice vedení tepla v hornině.

Přes tyto nedostatky je možno, jak dokládají uvedené příklady, vzhledem k poměrně dobré shodě výsledku výpočtu s kontrolními měřeními, najít pro uvedené modely řadu praktických uplatnění. Vzhledem k tomu, že dne 1. dubna 1978 vstoupil v platnost Bezpečnostní předpis pro jeskyně (ČBÚ 1977) ukládající organizacím, provádějícím zpřístupnění a spravujícím jeskyně již zpřístupněné, mimo jiné povinnost dbát na udržení původních klimatických podmínek, rozšíří se uplatnění modelů pravděpodobně zejména v této oblasti. Možnosti aplikací při studiu souvislostí mezi klimatickými podmínkami a původem sekundárních výplní a posuzování vhodnosti jeskynních prostor pro speleoterapii si vyžádají důkladnější rozpracování, avšak i v těchto směrech je možno předpokládat úspěšné řešení.

 

Literatura:

• Carslaw H.S., Jaeger J.C. (1946, 1959): Conduction of Heat in Solids. – Clarendon Press: 1—510. Oxford.
• Český báňský úřad (ČBÚ) (1977): Bezpečnostní předpis pro jeskyně. – ČBÚ, čj.4500/79/1977. Praha.
• Jančařík A. (1976a): Nástin dynamiky ovzduší v jeskyních na příkladu horních pater Koněpruských jeskyní. – Český kras, 1: 7—16, 4 přílohy. Beroun. [A5]
• Jančařík A. (1976b): K některým aspektům zpřístupnění Koněpruských jeskyní. – Sborník sympozia Komise pro speleoterapii UIS, Horný Hrádok (tč. v tisku).
• Jančařík A. (1977): Effect of Alternations of the External Air Pressure on the Climatic Regime of Caves. – Tarcus Proceedings on the occasion of the 7th International Congress of Speleology, Sheffield '77. Krasová sekce Praha – TIS – Svaz pro ochranu přírody a krajiny: 37—40. Praha.
• Kordos L. (1970): Klímamegfigyelések a barlangok bejárati szakaszában. – Karszt és barlang, 1970/1: 31—34. Budapest.
• Kordos L. (1972): Mikroklimavizsgálatok a Kevély-csoport néhány barlangjában. – Karszt és barlang, 1972/1—2: 5—12. Budapest.
• Kunský J. (1950): Kras a jeskyně. – Přírodovědecké nakladatelství: 1—163. Praha.
• Lysenko V. (1975): Changes in Cave Regime as a Consequence of General Public Accessibility (on the Example of Koněprusy Caves). – Annales de spéléologie, 30/4: 719—724. Moulis.
• Lysenko V. (1976): Změny klimatu v Koněpruských jeskyních v závislosti na jejich zpřístupnění. – Speleologický věstník, 7: 13—24.
• Piciocchi A., Utili F. (1975): La speleoterapia nella Grotta Giusti di Monsummano Terme. – Annuario Speleologico, 3(1974—1975): 91—98. Club Alpino Italiano Sezione di Napoli. Neapol.

 

Résumé

On the basement of relations /1/, /5/, /6/, /7/ and /8/ and simplifying suppositions:

• 1 – a simple tunnel come in consideration (Fig.1),
• 2 – air-flow is caused only by the different pressures of air columns having different temperature,
• 3 – temperature field is homogeneous in the profiles perpendicular to the air-flow direction,
• 4 – relation in changes of latent and apparent heat is constant,

there was elaborated the climatic model of the dynamic cave. Calculations are executed on the programable calculator WANG 2200. Calculated results 4/ and really measured values 1/, 2/, 3/ are presented on Fig.2. Differences are probably caused by the considered simplifying suppositions, especially by the supposition 3. Comparing the dependance of temperature on the distance from the intake entrance distinct differences can be determined only at the distance of 20—30 m (the second Kordos's zone). The model was utilized for the estimate of microklimate in the Koněprusy Caves before the caves have been made accessible for the public (Fig.4). After correction of some imperfections and after modification it is possible to suppose that the model will be of use not only in the case when considering man's interference with cave microclimate but also in speleotherapy and for studying of connections between the paleomicroclimatic conditions and the origin of the secondary fillings.