K dynamickému odporu proudění
Jiří Botur, Antonín Jančařík
(Český kras 6; str.53—57; Beroun 1981)
Pro studium pohybu tekutin (plynů a kapalin) je nutno znát mimo jiné dynamický odpor daného prostředí.
V jeskyních se jako proudící medium vyskytuje vzduch nebo voda. Pro tento případ je možno i vzduch považovat za nestlačitelný, a proto platí pro obě tekutiny stejné dynamické principy.
Odpor prostředí je do značné míry ovlivňován charakterem proudění. Existují dva druhy proudění – laminární a turbulentní. Pokud se jednotlivé proudnice navzájem kříží, jde o proudění turbulentní, v opačném případě o laminární.
Zákony pro proudění tekutin jsou vesměs empirické a vycházejí z experimentů v kruhových trubicích. Tak bylo m.j. zjištěno, že charakter proudění je ovlivňován vazkostí (viskozitou), rychlostí proudění a geometrií potrubí. Tyto tři veličiny v Reynoldsově vztahu informují o charakteru proudění, a to podle hodnoty Reynoldsova čísla Re:
/1/
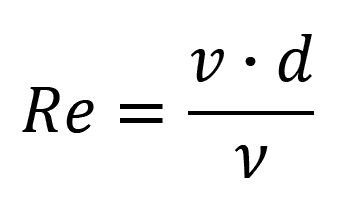
kde:
- v ... rychlost proudění [m.s−1],
- d ... charakteristický geometrický rozměr [m],
- ν ... ný, kinematická vazkost [m2.s−1].
Reynoldsovo číslo je bezrozměrné a jeho hodnota asi 2300 je udávána jako začátek přechodu mezi laminárním a turbulentním prouděním. Hranice mezi oběma druhy proudění není ostrá a dle údajů literatury se přechodové pásmo pohybuje podle různých podmínek (často uměle vytvořených) od 103 do 105.
Důležitou veličinou v Re je kinematická vazkost, určující charakter proudícího media. V každé tekutině totiž působí proti jejímu pohybu vnitřní tření. Jde o smykové tření mezi jednotlivými – pomyslnými – vrstvami tekutiny. Pro laminární proudění odvodil příslušný zákon Newton, když zjistil, že tečné napětí v tekutině je úměrné jejímu gradientu rychlosti. Konstantou úměrnosti je dynamická vazkost μ, která je s kinematickou vazkostí ve vztahu:
/2/
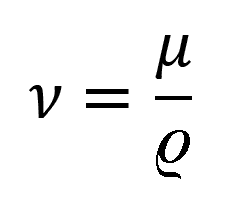
kde:
- ϱ ... ró, měrná hmotnost [kg.m−3].
Rozdělení rychlosti v kruhovém průřezu trubice je různé. Pro laminární proudění je prostudovali Hagen a Poiseuille. Výsledkem jejich studia je zákon, který lze vyjádřit vztahem:
/3/
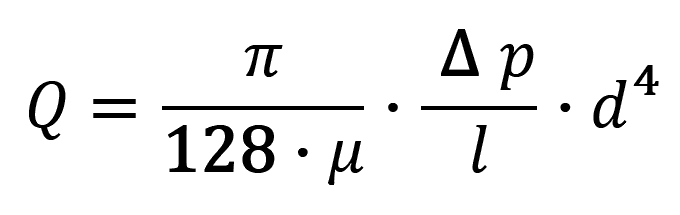
kde:
- Q ... objemový průtok tekutiny [m3.s−1],
- Δp ... tlakový rozdíl [Pa],
- l ... dráha proudění [m],
- d ... průměr trubice [m].
Tento vztah platí přesně pro kruhové potrubí. Aplikace na potrubí jiného geometrického tvaru je možná pomocí tzv. hydraulického průměru. Jde o veličinu, která určuje velikost kruhového potrubí, které má stejné hydraulické vlastnosti jako potrubí studované. Hydraulický průměr dh se vypočte z plochy protékaného průřezu F a plochy obtékaného obvodu O:
/4/
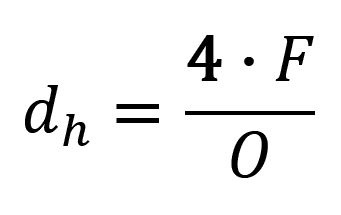
Odpor prostředí se projevuje energeticky ztrátou tlaku tekutiny. Obecně platí, že:
/5/
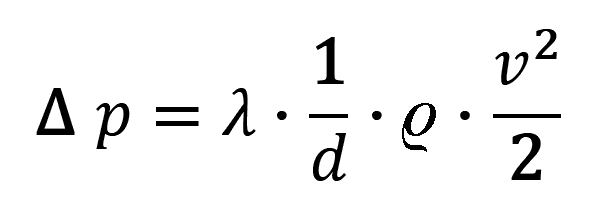
kde:
- λ ... součinitel tření [1].
Pro laminární proudění vychází s použitím vztahu /3/, že:
/6/
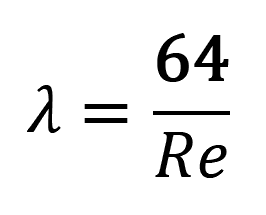
Pro turbulentní proudění jsou poměry podstatně složitější. Je tomu tak proto, že tření v tekutině není možno v tomto případě vyjádřit konstantou fyzikální, jako je tomu u Newtonova zákona. Aerodynamické poměry při turbulentním proudění jsou výrazně ovlivňovány poměrnou drsností stěn potrubí, které se definuje jako poměr mezi střední hodnotou výšky výstupků k na stěně potrubí a jeho průměrem.
Pro hydraulicky hladké potrubí existuje několik empirických vzorců, které se liší podle experimentálních podmínek jednotlivých autorů.
Např. BLASIUS (1911) uvádí pro Re < 80 000 vztah:
/7/
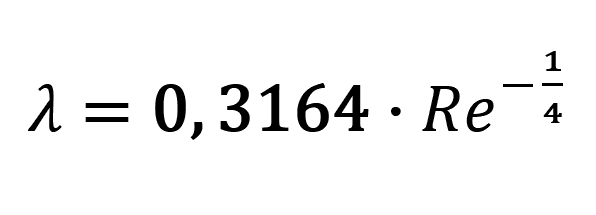
Nebo KÁRMÁN (1930) a NIKURADSE (1930) pro Re nejvýše dosažitelných hodnot:
/8/
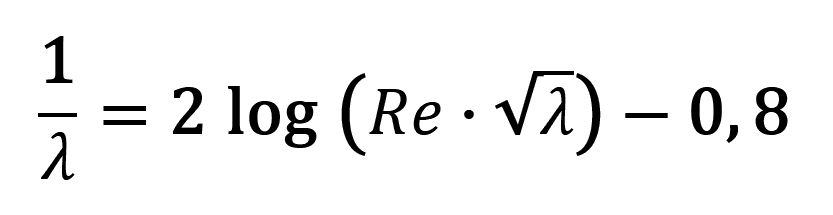
Od určité hodnoty Re je λ nezávislé na rychlosti proudění. Tato hodnota Re závisí na poměrné drsnosti stěn. V tom případě platí vztah (NIKURADSE 1930):
/9/
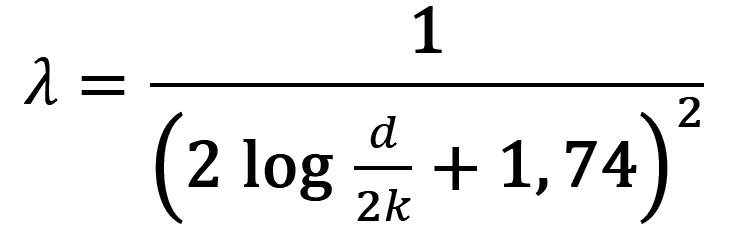
Jak je známo, je objemový průtok dán součinem plochy průřezu a střední rychlosti proudění.
Z toho potom plyne, že při laminárním proudění roste odpor prostředí s první mocninou rychlosti, při turbulentním proudění v hydraulicky drsných potrubích s druhou mocninou rychlosti. Je zajímavé, že v přechodové oblasti mezi laminárním a turbulentním prouděním může exponent rychlosti proudění přesáhnout hodnotu 2. Např. BATZEL a SCHMIDT (1952) uvádějí hodnotu 2,4.
Tato okolnost je významná pro přesnost určení tlakového spádu v chodbě s proudícím mediem o známém aerodynamickém odporu a objemovém průtoku. Většinou se vychází ze vztahu:
/10/
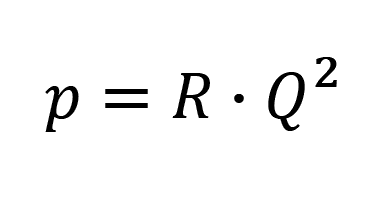
Vzhledem k tomu, že objemový průtok je v lineární závislosti na střední rychlosti proudění, znamená to, že podle charakteru proudění a stupně drsnosti stěn, nemusí být ve skutečnosti exponent u Q přesně roven hodnotě 2. Samozřejmě je vztah /10/ početně jednoduchý a navíc odpovídá většině skutečných případů. Pro přesná vyhodnocování je však nutné zamyslet se nad charakterem proudění, vlastnostmi obtékaného povrchu a požadovanou přesností. V některých případech bude nutné použít vztah /10/ ve tvaru:
/11/
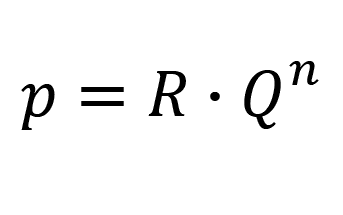
kde:
/12/
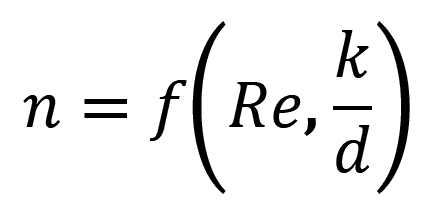
Při modelování proudění vzduchu v jeskyních může zanedbání uvedených skutečností vnášet do výpočtu chybu řádově se blížící skutečnému průtočnému množství. Stejně tak při posuzování průtoku vody např. syfony je třeba mít v patrnosti, že závislost mezi průtočným množstvím a tlakovým rozdílem (rozdílem hladin) není ani lineární ani kvadratická, ale obecně mocninná funkce, kde exponent n je funkcí Re a koeficientu drsnosti. Znamená to, že poměr změn hladin při změnách průtoku je (zejména při nižších průtocích) složitou, v praxi výpočtem obtížně vyjádřitelnou funkcí těchto dvou veličin.
Literatura:
- Blasius H. (1911): Das Ähnlichkeitsgesetz bei Reibungsvorgängen. – Physikalische Zeitschrift, 12: 1175—1177. Nakladatelství S.Hirzel. Leipzig.
- Nikuradse J. (1930): Über turbulente Wasserströmungen in geraden Rohren bei sehr grossen Reynoldsschen Zahlen. – Vorträge aus dem Gebiete der Aerodynamik und verwandter Gebiete, Aachen 1929: 63—69. Nakladatelství Springer. Berlin, Heidelberg.
- Kármán Th.von (1930): Mechanische Ähnlichkeit und Turbulenz. – Verhandlungen des 3. Internationalen Kongresses für technische Mechanik, Teil 1: 85—93, Stockholm.
- Batzel S., Schmidt W. (1952): Untersuchungen über die Wetterverzweigung unter Tage und ihre Vorausbestimmung mit Hilfe eines elektrischen Wettermodelles. – Glückauf, 88/19—20: 471—479. Essen (Ruhr).
- Smetana J. (1957): Hydraulika 1. – Nakladatelství ČSAV: 1—543. Praha.


