Použití geofyzikálních metod při průzkumu krasu

Seznámení se základy geofyzikálních metod průzkumu krasu

Libor Kraus, Stanislav Mayer

(Stalagmit 1988/3 {27}; str.3—31; Praha 1988)

 

Úvod

Tam, kde má speleologie delší tradici, dochází k vysokému stupni prozkoumanosti krasových oblastí. Spolu s tím a současně s pokrokem vědy a techniky používá speleologie nových vědních disciplín, které speleologický výzkum zkvalitňují a doplňují. V případech, kde klasické metody speleologického průzkumu jsou u konce svých možností nebo by jejich další nasazování bylo neefektivní, mohou netradiční metody přinést nové informace a zpětně v novém stadiu poznání objektu umožnit revizi nebo pokračování průzkumu klasickými metodami při vzájemném přínosu a obohacení poznatky všech zúčastněných vědních oborů.

Jednou z novějších disciplín používaných ve speleologii je užitá geofyzika. Jedná se o vědní obor, který využívá nových poznatků geologie, fyziky, elektroniky a hromadného zpracování dat. Současně je aplikovanou vědou, která studuje přirozená nebo umělá fyzikální pole, pokud mají význam pro řešení zadaného problému v rámci geologické struktury, lokality, oblasti nebo litosféry. Geofyzika využívá pole tíhové, magnetické, elektrické, elastického vlnění, radioaktivního záření a tepelné. Podle toho dělíme geofyzikální metody na gravimetrii, magnetometrii, geoelektriku, seismiku, radiometrii a geotermiku.

Geofyzikální metody mohou být použity podle podmínek a způsobu měření v různých variantách – letecké, pozemní, důlní, vrtní, pod mořskou hladinou apod. Každá z těchto variant má své přístrojové, metodické a interpretační zvláštnosti. Z hlediska použití rozlišujeme geofyzikální metody pro řešení otázek hlubinné stavby a strukturně geologických problémů, pro řešení problémů v inženýrské geologii a hornictví, v hydrogeologii, při průzkumu ložisek nerostných surovin apod.

Při průzkumu krasu má nejširší uplatnění geoelektrika, dále gravimetrie a geotermika a jen omezeně seismika s magnetometrií. Tato práce nedává přehled o celé šíři geofyzikálních metod, ale je jen stručnou ukázkou těch metod užité geofyziky, které se nejčastěji používají při průzkumu krasových jevů.

 

 

 

I. GEOELEKTRIKA

Elektrické vlastnosti hornin

Nejdůležitějším parametrem je měrný odpor ϱ (ró), v menší míře lze využít měření samovolně vznikajících filtračních potenciálů, polarizovatelnost η (éta), permitivitu prostředí ε (epsilon).

Měrný odpor je stanoven odporem krychle horniny o hraně 1 m a vyjadřujeme jej v Ω.m (ohm metrech, ohm.m). Je ovlivněn velkým množstvím faktorů – mineralogickým složením, porózitou, stupněm nasycení vodou a její mineralizací, strukturou a texturou hornin, teplotou a tlakem.

Odpory minerálů vykazují obrovské rozdíly v rozmezí 20 řádů. Avšak horniny v přirozeném prostředí mívají kontrast v odporech mnohem menší, zpravidla nepřevyšuje 4 řády. U hornin je důležitým faktorem stupeň nasycení vodou a mineralizace vody. Obecně lze konstatovat, že odpor stoupá se stupněm zpevnění horniny, se snižováním pórovitosti a s vysoušením horniny. Naopak odpor klesá se stupněm zvodnění a nasycení mineralizovanými roztoky a s navětráním a porušením horniny. U nezpevněných sedimentů odpor postupně klesá s přibýváním jemné frakce a zejména s rostoucím obsahem jílovité složky. Z běžných hornin mívají nejnižší odpory plastické jíly (někdy i prvé jednotky Ω.m). Mořská voda má méně než 1 Ω.m.

Teď obraťme pozornost k fyzikálním parametrům krasových struktur. Krasovou strukturou rozumějme geologický objekt vytvořený procesem krasovění se vším, co s ním souvisí. Krasovou strukturou jeskyně není jen volná dutina, ale patří k ní také jeskynní sedimenty, prostor zaplněný vodou, síť rozšířených puklin a embryonálních kanálků souvisejících s ní apod. Každá součást má jiné fyzikální vlastnosti. Vzduchová prostora má prakticky nekonečný odpor, ale většina ostatních částí je vodivější než pevný, nezkrasovělý vápenec. Navíc každá jeskyně či puklinka je stálou nebo občasnou drenáží vápencového masivu, splavují se do nich zvětraliny a humus.

Z toho vyplývá, že pouze veliká a mělce pod povrchem uložená jeskyně se může při uspořádání s optimálním hloubkovým dosahem projevit odporovým maximem. Většinou se však jeskyně projevují jako vodivé zóny, protože objem těch částí krasové struktury, které jsou vodivější než krasověním neporušený vápenec, bývá zpravidla mnohem větší nežli těch, které se mohou oproti svému okolí projevovat zvýšením odporu. Pruh zkrasovělého vápence se v geofyzikálním poli většinou projevuje jako vodivá zóna.

Přehled elektrických odporů hornin v jižní části Moravského krasu podávají tabulky 1 a 2. Představu o odporech si lze učinit ze všech řezů sestrojených z kvantitativní interpretace křivek VES (vertikální elektrické sondování; obr.7). V řezech jsou v každé vrstvě vyznačeny hodnoty interpretovaných odporů v Ω.m. Někde je uvedena značka pro nekonečný odpor. To je většinou způsobeno krátkou délkou sondážní křivky tam, kde se na povrchu nachází mocnější vodivá vrstva, a nebo jinými vlivy, které deformují proudové pole mezi elektrodami. V takových případech se vyšší odpory často jeví jako nekonečné, i když ve skutečnosti mají reálnou hodnotu.

V severní části Moravského krasu rozlišují Daňko, Blížkovský, Ryšavý (1966) vápence podle odporu do tří skupin:

Odpor rudických vrstev se pohybuje od 140 do 320 Ω.m.

V tabulce 1 jsou hodnoty karbonátů určeny z malého množství hodnot. J. Hruška (1986) uvádí mnohem jednodušeji rozpracovanou tabulku z jiného úseku jižní části Moravského krasu. Hodnoty odporů jsou však určeny interpretací VES a informace o horninách, ke kterým se vztahují, jsou převzaty z dokumentace technických prací a popisu výchozů (tab.2).

 

Tabulka 1. Odpory některých hornin v jižní části Moravského krasu (Hašek, Dvořák 1972):

Geologický útvar Horniny Měrný odpor ϱ
[Ω.m]		 Počet hodnot
Kvartér hlíny, svahoviny 7—100 85
Neogén jíly (štěrky) 3—40 (50—200) 88 (36)
Karbon slepence, droby nad 300 12
pískovce, břidlice 40—370 82
Devon Vápencové písčité brekcie:
vápence s obsahem rohovců 500—1000 3
zbřidličnatělé vápence až slínovce 100 2
bituminózní vápence s břidlicemi 40—60 5
Vápence říčské:
nezkrasovělé organodetritické vápence 4000—5000 5
nezkrasovělé s obsahem rohovců 2000—3500 4
podrcený vápenec asi 1500 2
silně porušený vápenec asi 500 9
silně porušený jílovitý vápenec s břidlicemi 150—400 5
Vápence vilémovické:
nezkrasovělé, pevné vápence 1500—300 8
vápence porušené, zkrasovatělé 600—1200 9
silně porušené, zkrasovatělé s jílovito-písčitou výplní 150—500 11
Devonská bazální klastika:
pískovce, slepence 100—500 —
Krystalinikum — nad 1000 10

 

 

Tabulka 2. Odpory hornin z oblasti Horákov – Mokrá (Hruška 1986):

Geologický útvar Horniny Měrný odpor ϱ
[Ω.m]
Neogén jíly, písky 10—130
Karbon droby, slepence (droby nejčastěji 200, slepence 450) 110—690
břidlice 250—400
Devon vápence nerozlišené (rozsah hodnot) 150—27000
silně zkrasovělé a porušené vápence 150—400
středně zkrasovělé 300—600
slabě zkrasovělé 500—800
nezkrasovělé rozpukané 800—2000
nezkrasovělé pevné (nejčastěji) 2000—27000

 

Předložené informace o odporech hornin nejsou zdaleka vyčerpávající a přesto zřetelně poukazují na široký rozsah odporů pro karbonáty. Rovněž poukazují na nejednoznačnost interpretace tam, kde se fyzikální vlastnosti různých hornin překrývají.

 

Přehled geoelektrických metod, o kterých zde bude zmínka:

 

I.A.a)1. Odporové profilování

Je jednou ze základních geoelektrických metod, kterou lze praktikovat v mnoha variantách. Bohatost měření spočívá v různých možnostech uspořádání elektrod. U všech odporových měření je nutno elektrické pole vytvořit. Ty elektrody, jimiž zavádíme do země proud a jimiž elektrické pole vytváříme, nazýváme elektrody proudové a označujeme písmeny A, B, ... Elektrický potenciál nebo jeho gradient měříme na potenčních (měřících) elektrodách a označujeme je M, N, ... Bod zápisu (místo k němuž vztahujeme naměřenou hodnotu) je u symetrických uspořádání definován středem soustavy elektrod, u nesymetrických středem potenčního dipólu anebo polohou pohyblivé potenční elektrody. Velikost hloubkového dosahu určuje vzdálenost proudových elektrod A, B. Hloubkový dosah většinou odpovídá třetině až čtvrtině vzdálenosti AB. Pro profilování je charakteristické to, že uspořádání elektrod je většinou stálé, podmínky vytváření a měření elektrického pole jsou tedy zhruba konstantní, uspořádání má přibližně konstantní hloubkový dosah a naměřené hodnoty ϱz jsou pak odezvou změny elektrického odporu ϱ především v prostoru mezi měřícími elektrodami MN. Dostáváme tak obraz o odporech v horizontálním směru podél profilu a zhruba ze stejné hloubky. Profilování se proto používá především pro vyhledávání svislých odporových rozhraní (odpor. kontaktů), rozhraní ve tvaru stupně, izometrického tělesa (koule, hranolu), svislé mocné nebo tenké desky (tenká deska je taková, která je tenčí než vzdálenost MN a obráceně), či horizontálního dlouhého válce (obr.1).

 

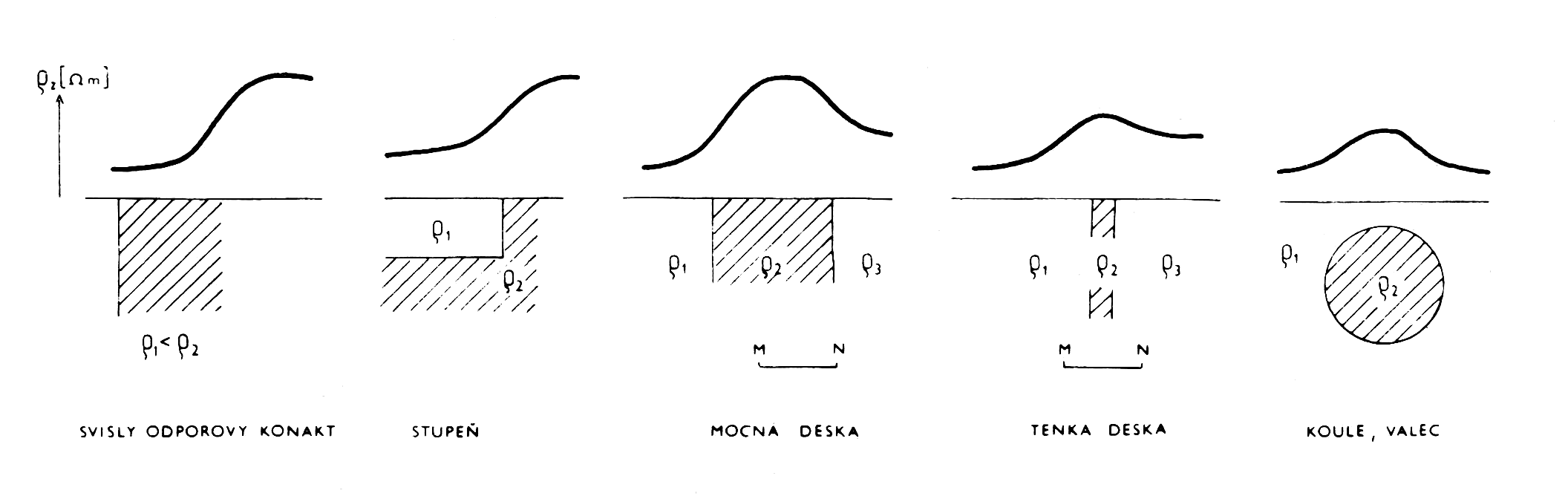
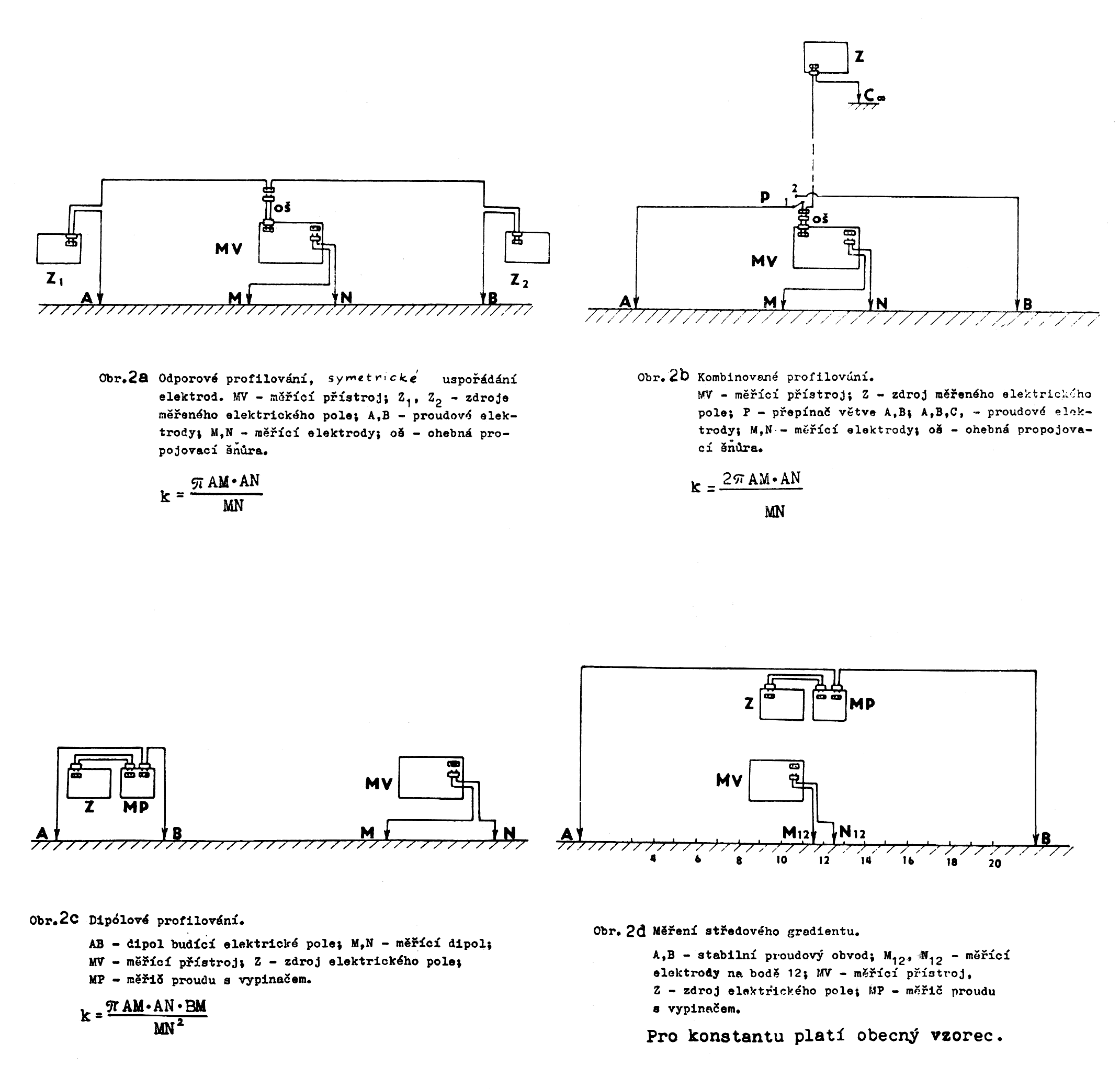
Obr.1: Některé typy odporových rozhraní a charakter tvaru ϱz pro symetrické odporové profilování – SOP (ϱ1<ϱ3<ϱ2).

 

 

Obr.2: Schéma nejčastějšího uspořádání elektrod a zapojení aparatury.

 

 

Na obrázku 2 jsou schémata čtyř nejčastějších uspořádání elektrod užívaných při odporovém profilování. Odpor se počítá z obecně platného vzorce pro všechna uspořádání odvozeného z Ohmova zákona:

 

 

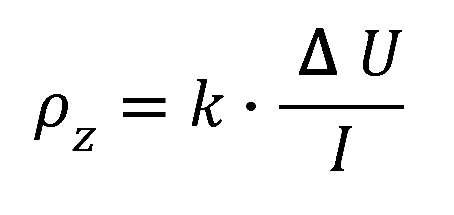
kde:

 

 

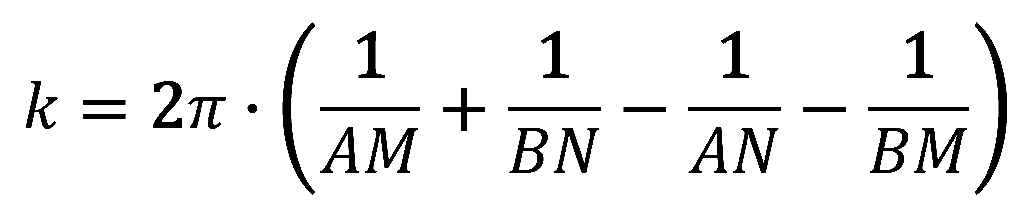
U každého z těchto uspořádání má elektrické pole vytvořené proudovými elektrodami jiný tvar. Proto jedna a tatáž nehomogenita vyvolá u každého uspořádání jinou deformaci pole, to má pokaždé jiný výsledný tvar a proto má každé uspořádání svůj charakteristický tvar křivek. Z toho důvodu se každé uspořádání hodí pro vyhledávání jiného anomálního objektu. Na obrázku 3 a 4 je ukázka, jak vodivé objekty různých tvarů deformují homogenní proudové pole (pole párových elektrod), proudové pole bodového zdroje a pole dipólu. Z obrázku je patrno, že kolmou, tenkou, vodivou deskou není proudové pole uspořádáním ve formě symetrického odporového profilování a středového gradientu podstatně ovlivněno a že podobný objekt lze těmito dvěma způsoby profilování jen těžko vyhledat. Vodivá tělesa izometrických tvarů a mocné vodivé desky lze vyhledávat všemi typy uspořádání.

 

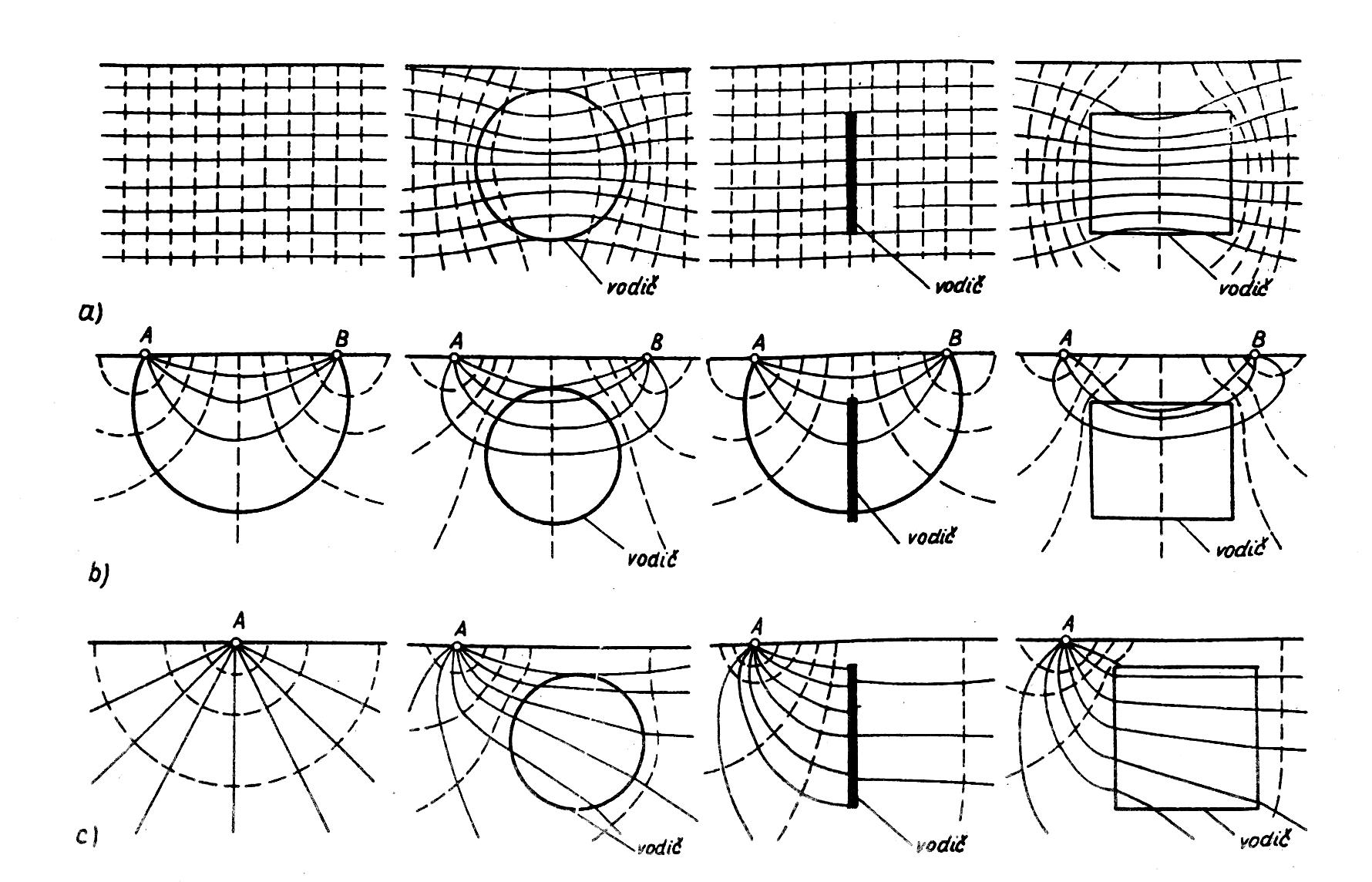
Obr.3: Zkreslení normálního pole vodivou nehomogenitou: a) homogenní proudové pole zkreslené vodivou koulí a vodivou deskou, b) pole dvou párových elektrod – symetrická uspořádání, c) pole bodového zdroje – kombinované profilování (Gruntorád, Karous 1972).

 

 

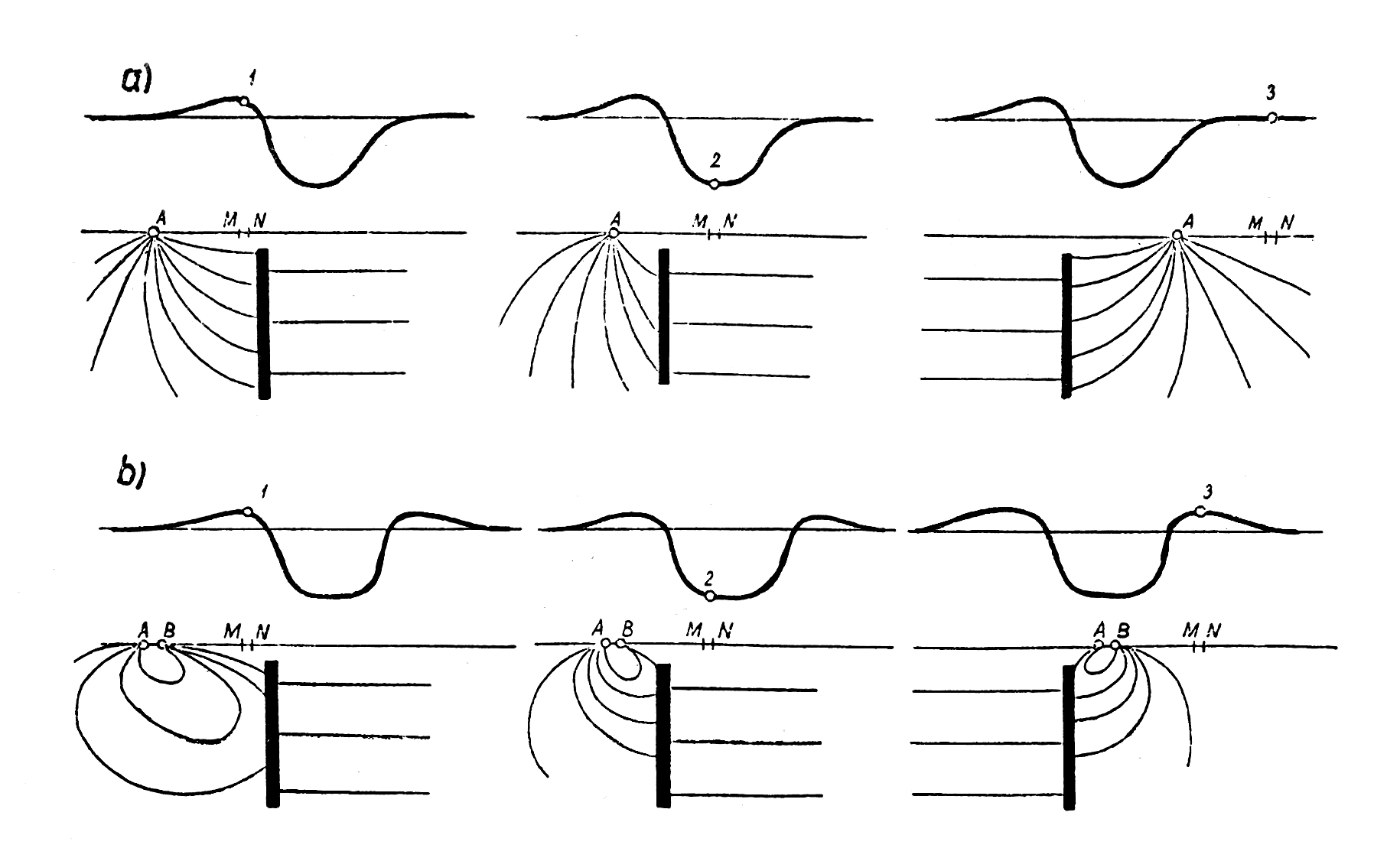
Obr.4: Změna zdánlivého měrného odporu při různých polohách elektrody nad vodivou deskou: a) tříelektrodové gradientové uspořádání, b) dipólové osové profilování (Gruntorád, Karous 1972).

 

 

Jinak je tomu v případě nevodivého tělesa. Objekt tvaru tenké desky nebo zploštělého elipsoidu lze snadno vyhledat, je-li uložen větší plochou kolmo k proudovým liniím. Je-li uložen podél nich, je jeho vyhledávání při všech typech uspořádání velmi obtížné. Právě vzduchem vyplněný prostor jeskynní dutiny mívá často tvar dlouhého (z hlediska dosahu metody nekonečného) vodorovně uloženého eliptického válce či hranolu s malým vertikálním rozměrem. K obtížnosti vyhledávání takových objektů přistupuje skutečnost, že nevodivé struktury jsou odporovými metodami ještě z jiných důvodů hůře sledovatelné než vodivé.

 

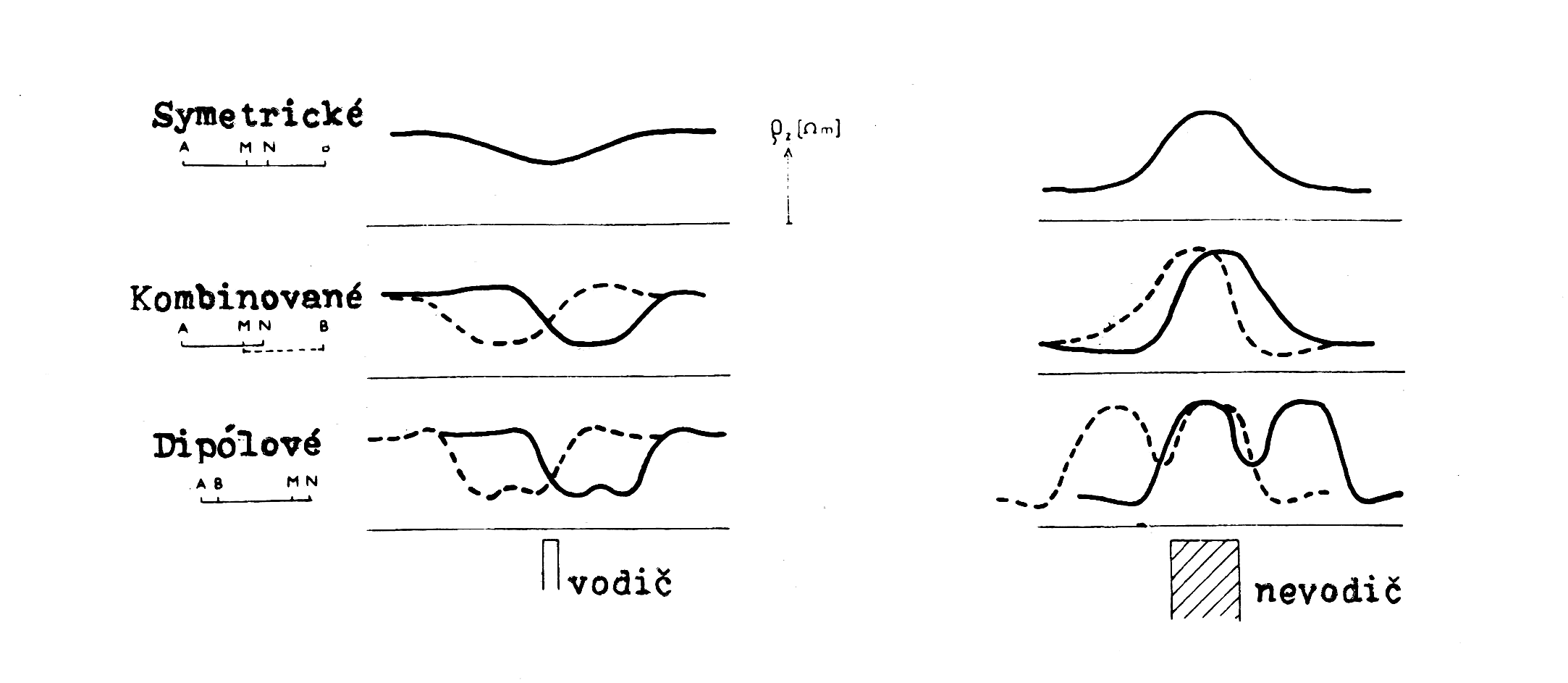
Obr.5: Charakteristické tvary odporových křivek pro různá uspořádání nad vodičem i nevodičem.

 

 

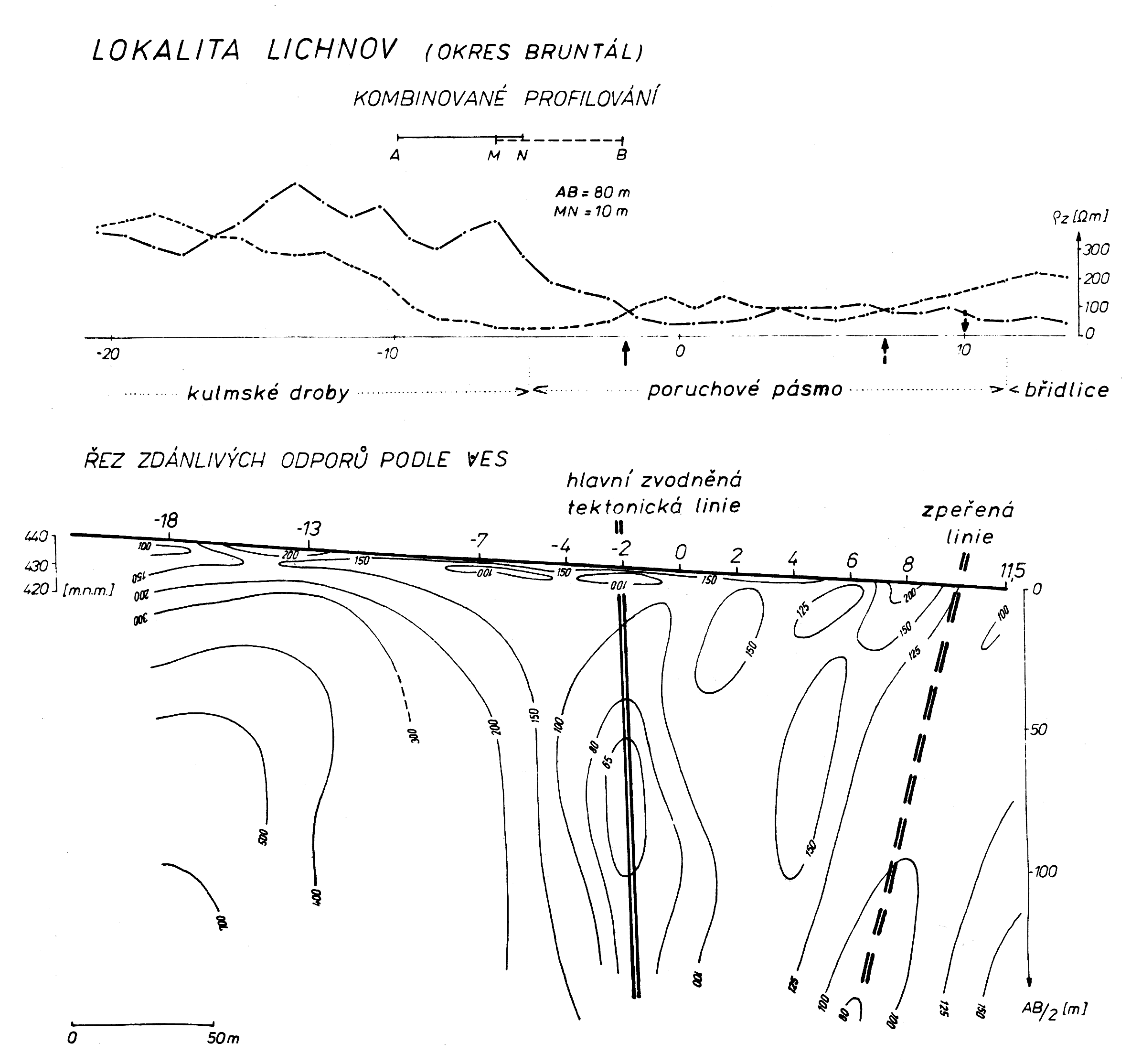
Obr.6: Schéma dokumentuje vyhledávání vlastního tělesa zvodněné tektonické linie v cca 160 m širokém poruchovém pásmu kombinovaným profilováním. Uspořádáním ve formě symetrického odporového profilování (SOP) by to nešlo (tenká, svislá, kolmá, vodivá deska). Nalezli bychom jen rozsah poruchové zóny (křivka SOP se získává zprůměrováním hodnot odporu obou větví kombinovaného profilování /KP/). Výsledek VES ve formě řezu ϱz při rovnoběžném roztažení s předpokládanou tektonikou (tenká, svislá, podélná, vodivá deska) zřetelně určuje polohu a směr sklonu hledaných struktur.

 

 

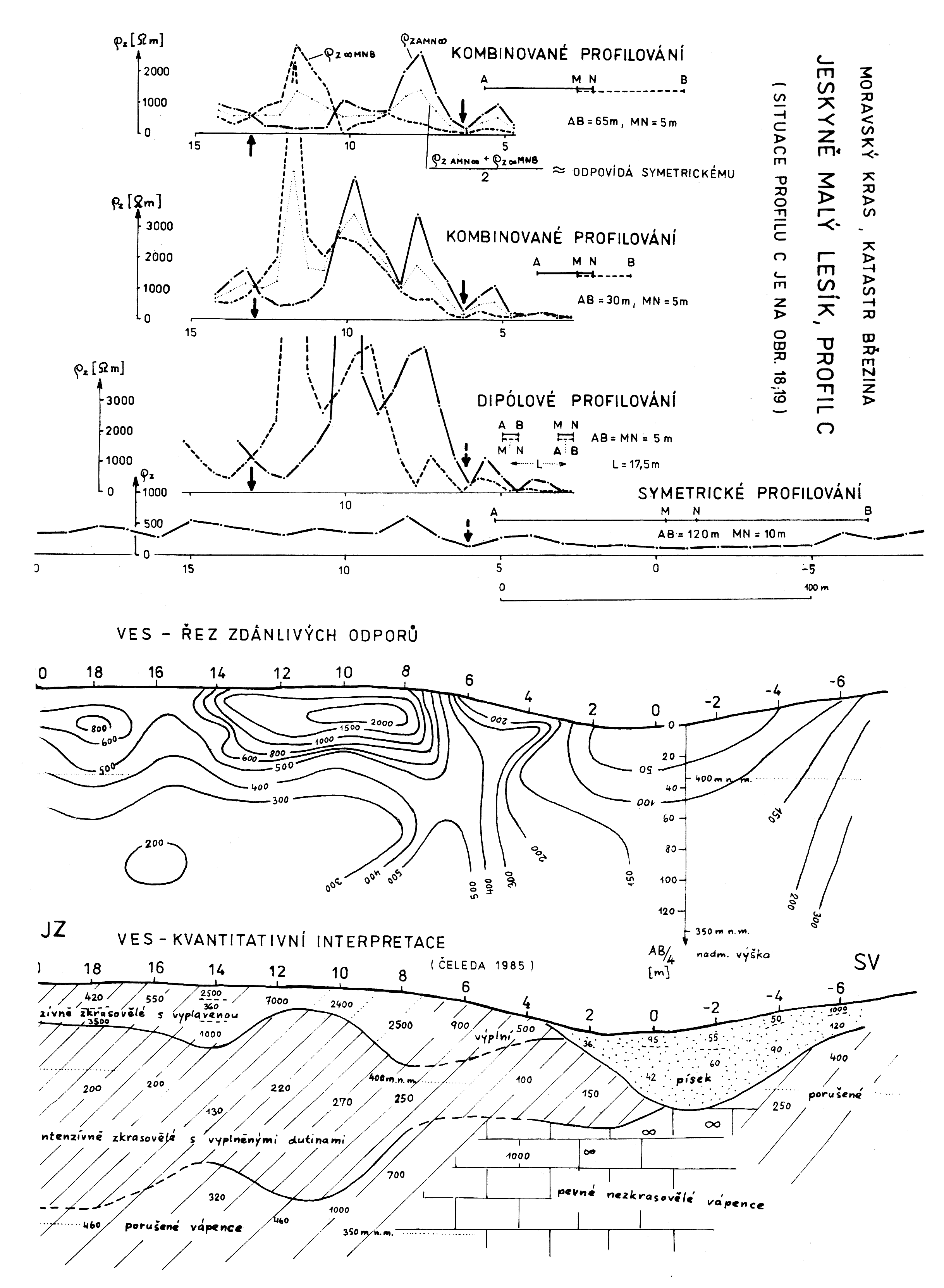
Obr.7: Odporové křivky čtyř různých uspořádání odporového profilování na profilu C ukazují na význam termínu zdánlivý měrný odpor (ϱz). Lokální vodič na metráži 13 opět není symetrickým uspořádáním vyhledatelný. Výsledky VES poukazují na intenzivní zkrasovění vápenců od povrchu až po nadmořskou výšku 355—400 m (od JZ k SV). Přitom spodní část vykazuje nízké odpory v důsledku zaplnění krasových dutin, kanálků a puklin přeplavenými jílovitými sedimenty. Vysoké odpory při povrchu reprezentují geoelektrickou vrstvu, ve které jsou vodivé výplně z vápenců vyplaveny. Řez ϱz dosti dobře odpovídá výsledné kvantitativní interpretaci.

 

 

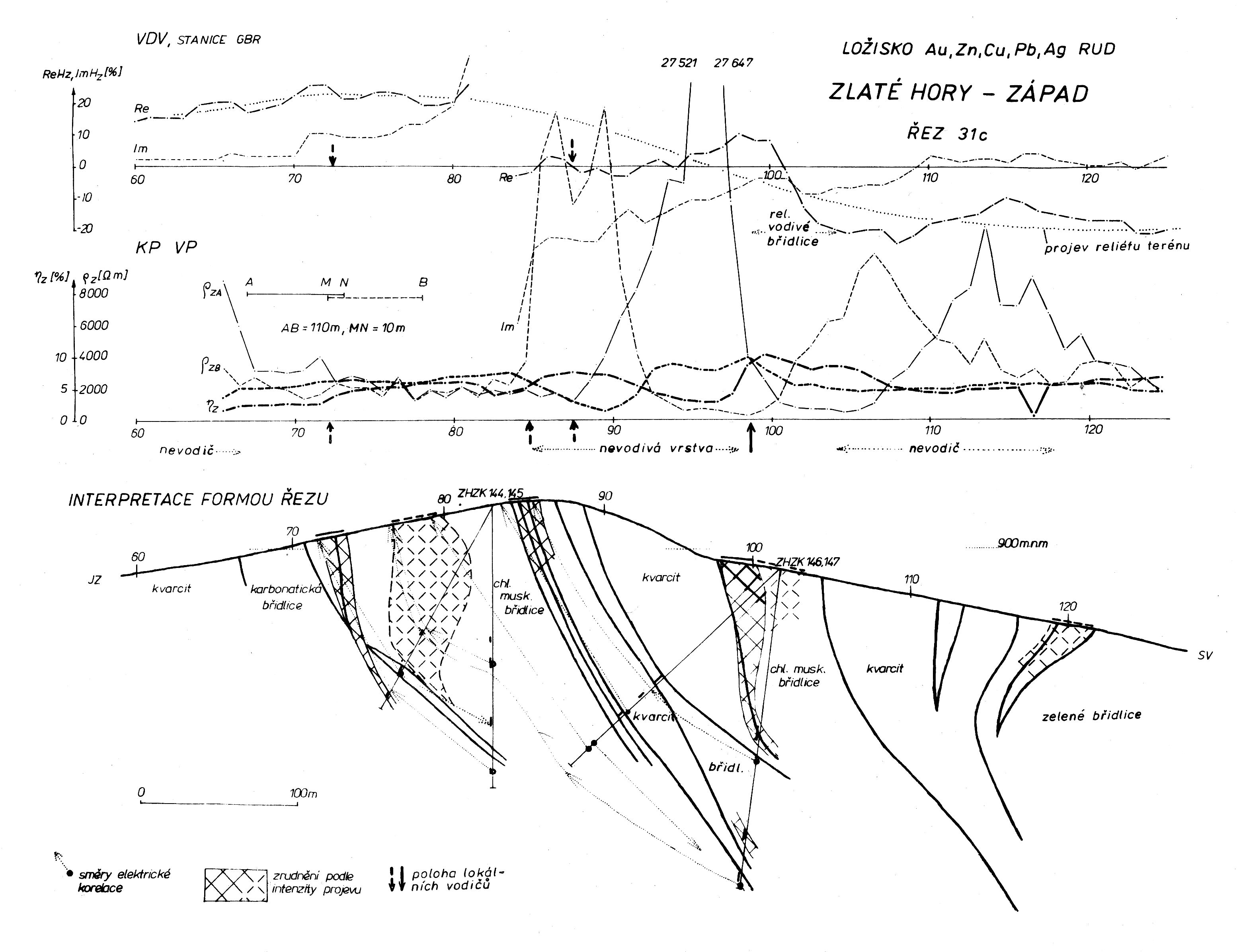
Obr.8: Všimněme si projevu tří nevodivých vrstev na odporových křivkách KP (tence kreslené). Projev lokálních vodičů je často díky nevodičům skrytý a posunutý. Ve výsledcích měření metodou VDV se mocná vrstva břidlic mezi dvěma nevodiči projevuje výraznou indikací vodivosti. Drobné lokální indikace vodivosti jsou na metráži 72,5 a 87,5. Vyhlazením křivky ReHz získáme regionální anomálii způsobenou hřebenem Příčné hory (tečkovaně). Geologický řez je sestrojen podle informací z vrtů a nejrozšířenějších měření metodou vyzvané polarizace.

 

 

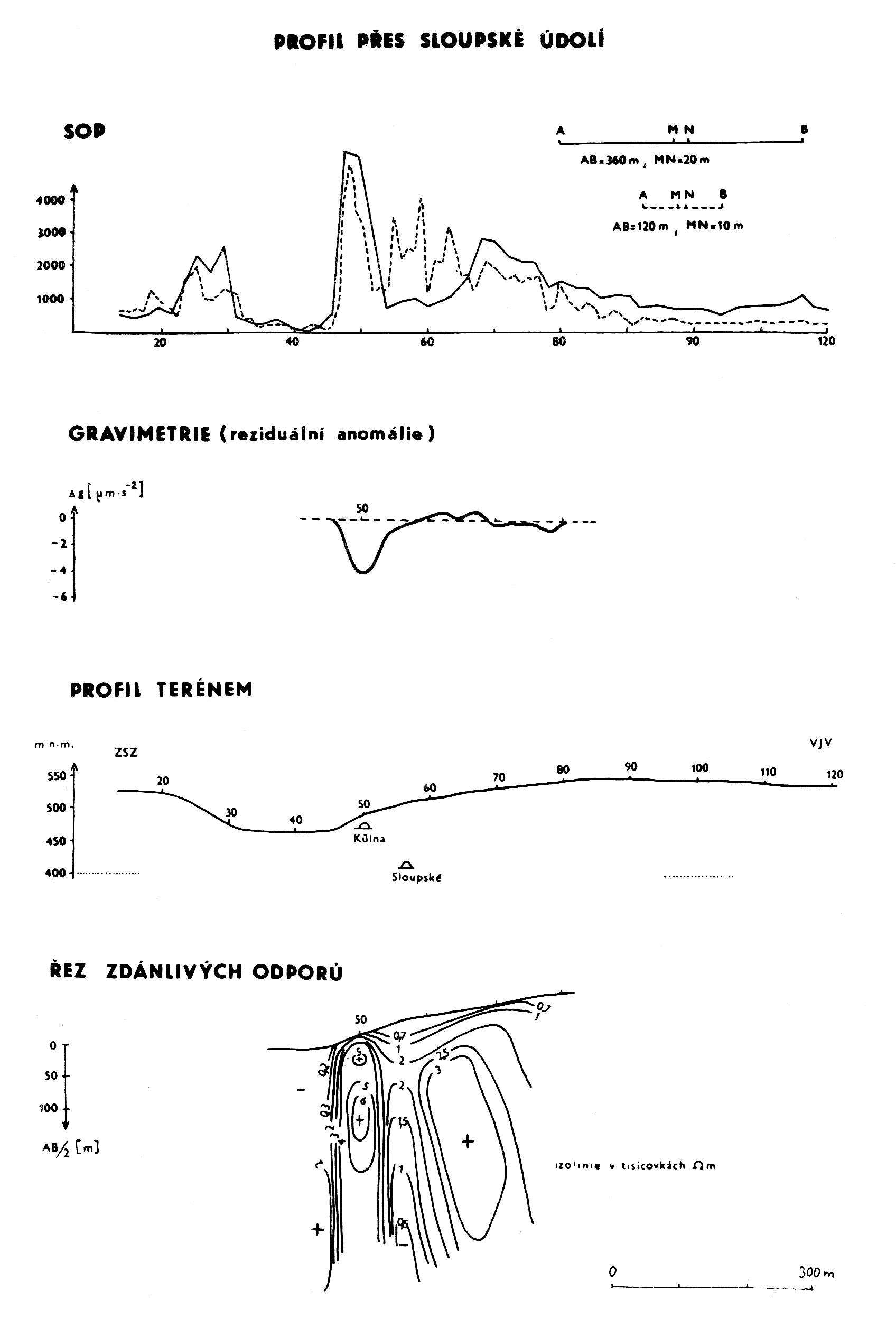
Obr.9: Výsledky na profilu přes Sloupské údolí (Daňko, Blížkovský 1968): Symetrické profilování se dvěma rozestupy udává plošný rozsah neogenní výplně Sloupského údolí (32—45) a vymezuje prostor hlubokého rozsáhlého zkrasovění v okolí spodních pater Sloupských jeskyní (53—64). Reziduální tíhová anomálie signalizuje nad jeskyní Kůlnou úbytek hmoty (volný prostor jeskyně a její sedimentární výplň). Řez ϱz je formován výplní Sloupského údolí, dutinou Kůlny (drobné maximum na metráži 50) a hlubokým zkrasověním v okolí spodních pater Sloupských jeskyní.

 

 

I.A.a)2. Vertikální elektrické sondování

Vertikální elektrické sondování (VES) spočívá ve studiu naměřené sondážní odporové křivky. Při měření se používá Schlumbergerova symetrického uspořádání (stejné uspořádání jako pro SOP, ale při zachování podmínky, že AB ≥ 5 MN). Bod zápisu (místo, ke kterému vztahujeme naměřenou hodnotu) se nemění a leží ve středu potenčního dipólu MN. Roztahováním proudových elektrod po přímce na obě strany od potenčního dipólu postupně zvětšujeme hloubkový dosah měření a získáváme tak obraz o změně elektrického odporu ve vertikálním směru. Z toho vyplývá, že sondování je vhodné především pro sledování odporových rozhraní ve vodorovně zvrstveném prostředí.

Příklad sondážních křivek je na obr.10. Jedná se o závislost naměřeného odporu ϱz na polovině rozestupu proudových elektrod AB vynesenou v bilogaritmickém papíru o modulu 6,25 cm. Aby bylo na měřících elektrodách MN zajištěno dostatečně velké čtení hodnot ΔU je nutno po určité době i mezi nimi zvětšovat vzdálenost. Snažíme se ale zachovat podmínku, aby AB ≥ 5 MN. Body změřené na jednom rozestupu MN se navzájem propojí. Při přechodu na větší MN se dva body převazují a měří se další část sondážní křivky. Nespojitost křivek při různých MN je způsobena zčásti jiným hloubkovým dosahem, ve větší míře však odporovými nehomogenitami v blízkosti MN. Křivky je zvykem vynášet tak, jakoby se skutečně jednalo o sondu.

Pro účely interpretace rozlišujeme křivky podle počtu geoelektrických vrstev, které se v rámci hloubkového dosahu měření podílejí na tvaru křivky, na křivky dvouvrstevné, trojvrstevné a vícevrstevné. Každou vícevrstevnou lze pak rozdělit na trojvrstevné. Obrázek 5 ukazuje základní typy dvou- a trojvrstevných křivek.

Některé parametry zjišťované z křivek jsou znázorněny na obr.11. Písmena h1 a ϱ1 označují mocnost a odpor první geoelektrické vrstvy. Podobně hi a ϱi jsou mocnosti a odpor i-té vrstvy. Sumární mocnost až k bázi i-té vrstvy je vlastně hloubka její spodní plochy od povrchu, tu označujeme jako mi.

 

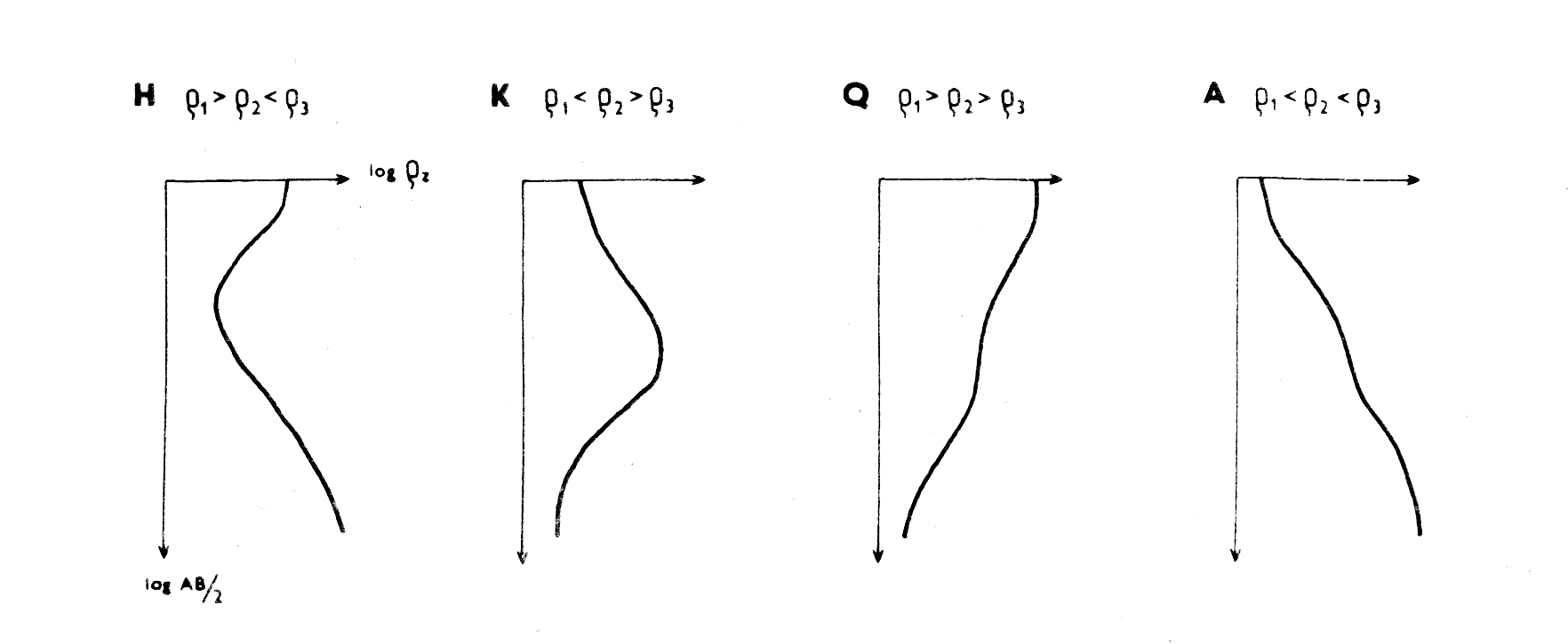
Obr.10: Typy trojvrstevných křivek.

 

 

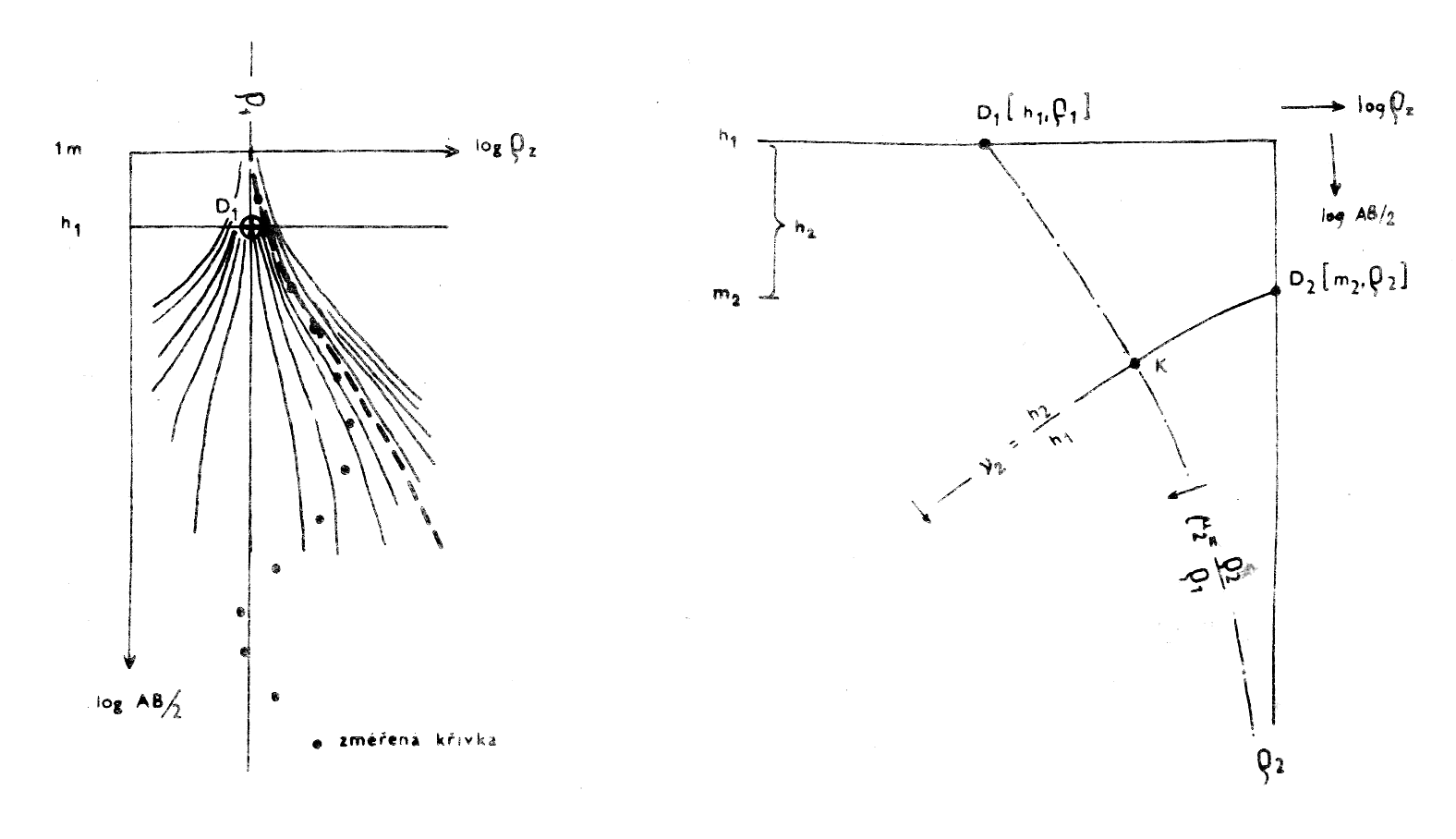
Obr.11 a 12:
11 – vlevo: Nalezení bodu D1 [h1, ϱ1];
12 – vpravo: Postup nalezení ekvivalentního bodu a parametrů druhé vrstvy.

 

 

Interpretace sondážních křivek

Rozlišujeme dva základní druhy interpretace – kvalitativní a kvantitativní.

a) Kvalitativní interpretace je interpretačním postupem, kdy nehledáme skutečné parametry geoelektrických vrstev (h, ϱ, m), ale pracujeme se zdánlivými odpory ϱz. Často jsou sestrojovány řezy zdánlivých odporů (obr.6, 7, 9), které zobrazují rozložení odporu ve vertikálním řezu. Vlastně se jedná o izolinie naměřených odporů ϱz ve svislé rovině. Odpory se v praxi většinou přisuzují hloubkám AB/2. Reálnější představu však podává řez, kde jsou hloubky vztahovány k AB/4 až AB/6. Někdy může být výsledek zobrazený v řezu zdánlivých odporů dostatečný a není třeba dalšího zpracování.

Jinou formou kvalitativní interpretace jsou mapy izolinií ϱz pro některý stanovený rozestup AB/2. Takový obrázek je ekvivalentní mapě izolinií ϱz sestrojené z měření formou SOP se stejným uspořádáním. Z křivek VES lze sestrojovat mapy izolinií jiných parametrů, například ϱz max, ϱz min, ϱz i-té vrstvy, podélné vodivosti S, příčného odporu T.

b) Při kvantitativní interpretaci jsou sondážní křivky podrobovány analýze, pomocí níž se snažíme získat interpretované hodnoty ϱ, h, m, které se blíží skutečným. Interpretuje se pomocí strojně početních metod, srovnáváním se souborem teoretických křivek, pomocí transformace křivek.

Při srovnání naměřených křivek s teoretickými lze postupovat několika způsoby. Nejjednodušší případ nastane, odpovídá-li naměřená křivka dvouvrstevnému prostředí. Pak ji stačí překreslit na průsvitku a za rovnoběžnosti os nalézt nejlepší shodu s křivkami na obr.13. Počátek – bod D1 – průsečík přímek ϱ1, h1 udává parametry 1. vrstvy, asymptota udává odpor ϱ2 (obr.11). Bod D1 a polohu asymptoty si poznačíme. Všechny tři hledané parametry (ϱ1, h1, ϱ2) odečteme po přiložení průsvitky s interpretovanou křivkou na bilogaritmický papír.

Dále si naznačíme postup interpretace trojvrstevných křivek pomocí souboru křivek dvouvrstevných. Počátek trojvrstevné naměřené křivky ztotožníme s dvouvrstevnou a najdeme tak ϱ1, h1, ϱ2. Pak přiložíme průsvitku s interpretovanou křivkou na pomocný nomogram pro hledání bodu H nebo K, Q, A (podle typu křivky, viz obr.10) a obkreslíme křivku o modulu μ2=ϱ2/ϱ1 (obr.12). Ta prochází bodem D1 o souřadnicích ϱ1, h1, ale také na ní leží pomocný bod H nebo K, Q, A. Jedná se o body, které určují parametry tzv. ekvivalentní vrstvy, která pro velké rozestupy AB/2 nahrazuje projev prvních dvou vrstev a vytváří nový počátek pro ztotožnění koncové části trojvrstevné křivky s některou z dvouvrstevných. Proto posunujeme interpretovanou křivku na průsvitce po souboru dvouvrstevných křivek při zachování rovnoběžnosti os tak, aby čerchovaná čára μ2 procházela počátkem (bodem o souřadnicích ϱ1, h1), dokud se koncová část interpretované křivky nesblíží s některou z dvouvrstevných. Tím jsme nalezli pomocný bod H, K, Q nebo A. Asymptota dvouvrstevné křivky současně určuje hodnotu ϱ3, tedy odpor třetí vrstvy. Hloubku báze druhé vrstvy, hodnotu m2=h1+h2 určíme zpětným přiložením na nomogram pro hledání pomocného bodu, přičemž křivka ν2 (ný), která jím prochází, vytíná na přímce ϱ2 hodnotu, která po přenesení na průsvitku a odečtení na bilogaritmickém papíru udává hloubku m od povrchu. Určením ϱ1, ϱ2, ϱ3, h1, m2 je interpretace trojvrstevné křivky hotova. Čtyřvrstevné a vícevrstevné křivky se interpretují postupně po částech. Jejich interpretace pomocí křivek dvouvrstevných je v případě tenčích vrstev značně nepřesná. Interpretace pomocí trojvrstevných křivek je přesnější. Vyžaduje však především vlastnictví souboru těchto křivek (bývá jich kolem 3000).

 

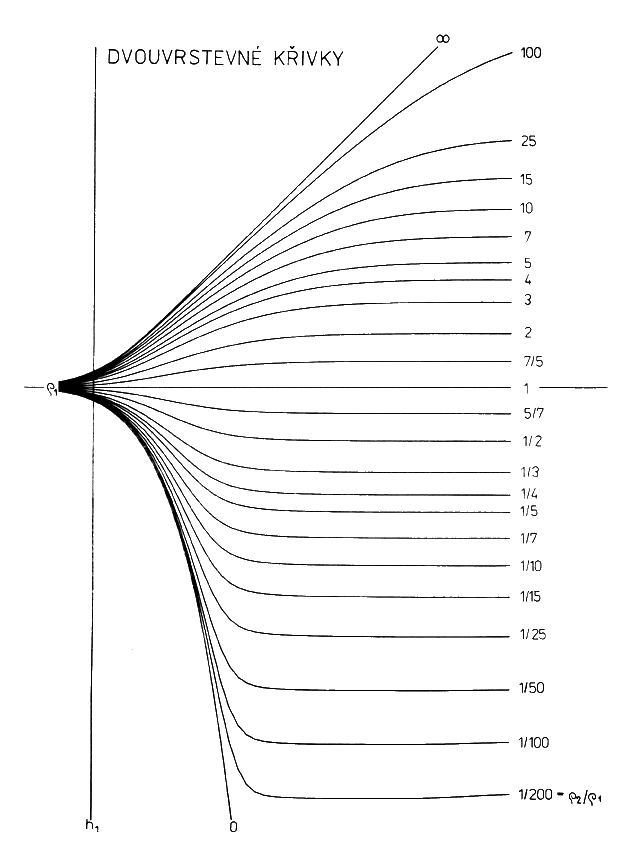
Obr.13: Dvouvrstevné křivky.

 

 

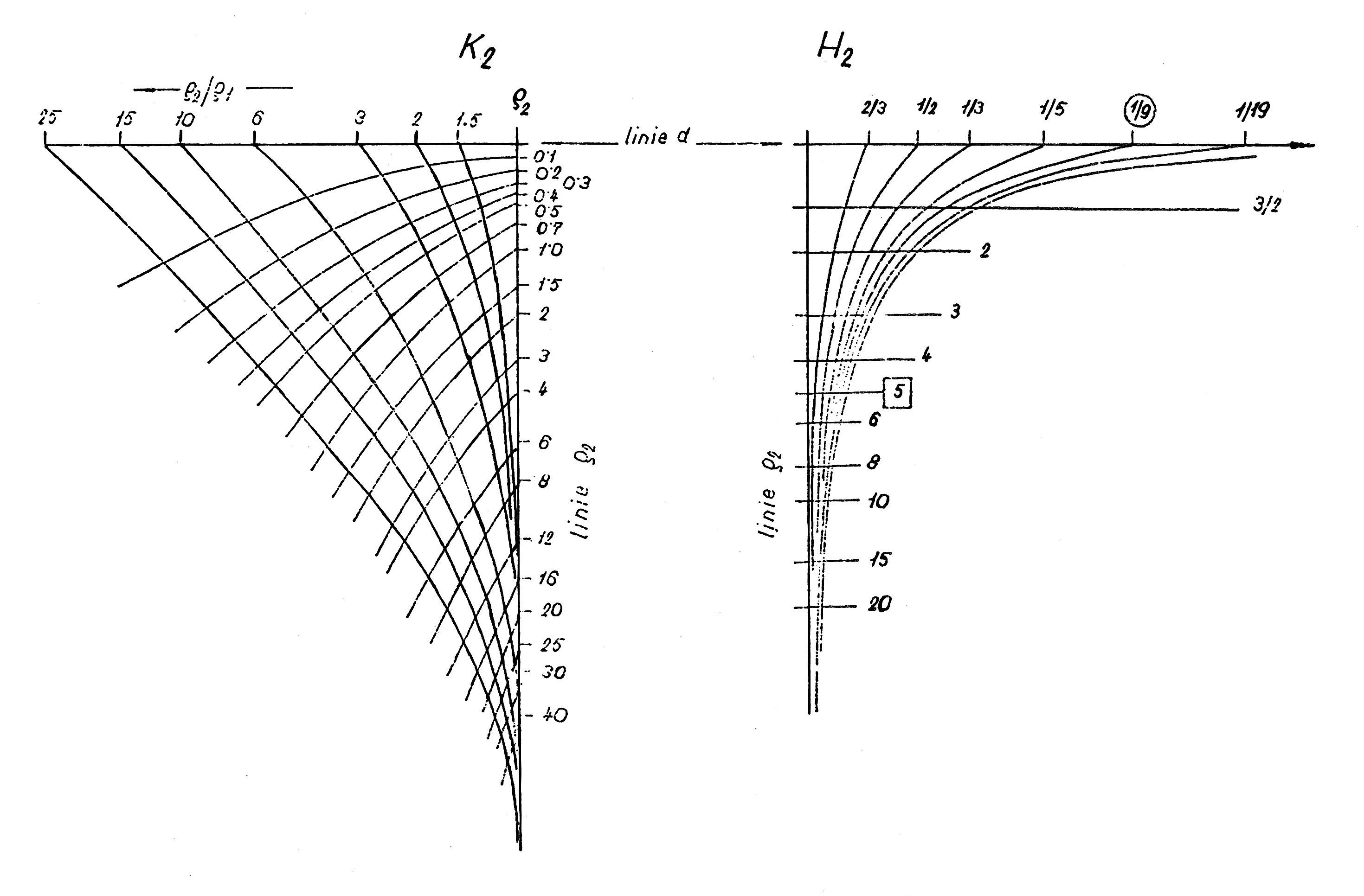
Obr.14: Nomogramy pro hledání ekvivalentních bodů (Karous 1977).

 

 

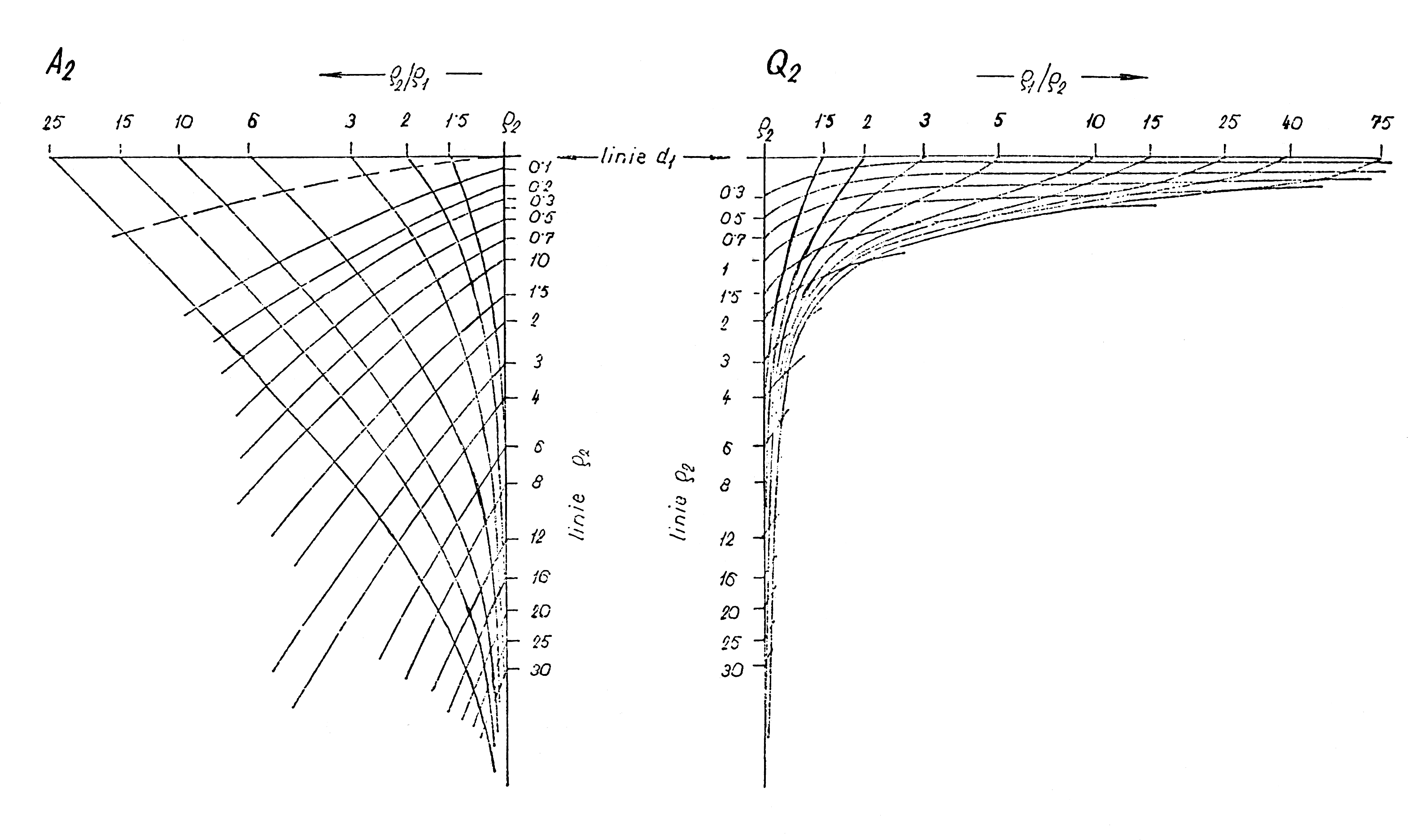
Obr.15: Nomogramy pro hledání ekvivalentních bodů (Karous 1977).

 

 

I.A.b) Metody potenciálové

V této skupině metod má pro účely průzkumu krasu význam především metoda nabitého tělesa (NT). Principem je studium elektrického pole v okolí bodového samostatného zdroje elektrody A. Ta se zpravidla uzemňuje do hledaného vodivého geologického objektu (rudní těleso, vodivé jeskynní sedimenty). Druhá proudová elektroda B se dává do takové vzdálenosti, aby už neměla na měření vliv. Říká se o ní, že je v „nekonečnu“. Stačí, aby byla nejméně 5× dále než je největší přímá vzdálenost od elektrody A k nejvzdálenějšímu místu na území, v němž bude měření prováděno.

Přístrojové vybavení je úplně stejné jako u odporových měření. Rozdíl je v tom, že výsledkem měření není elektrický odpor, ale křivky nebo izolinie buď vlastního potenciálu nebo jeho gradientu (spádu). Proudový a potenční obvod jsou zpravidla odděleny. V proudovém okruhu AB měříme množství protékaného proudu. Mezi elektrodami MN měříme potenciál (potenciálový způsob měření, viz obr.16), v případě dvou blízkých elektrod (dipólu) měříme rozdíly napětí mezi MN – gradient (gradientový způsob měření). Při měření gradientu potenciálu jsou výsledky přesnější. Navíc sumací hodnot gradientu lze sestrojit křivku potenciálu na daném profilu a při převazu celého území příčným profilem je možno vykreslit i ekvipotenciální linie, které dávají celkový obraz o tvaru elektrického pole jako by bylo použito potenciálového způsobu měření. V homogenním izotropním prostředí se kolem bodového zdroje tvoří ekvipotenciály kulového tvaru, které by v řezu terénem měly mít tvar kružnic. V reálném prostředí je elektrické pole deformováno odporovými nehomogenitami. Podle protažení a zředění izolinií lze vysledovat tvar a průběh vodivých struktur. Určitou předností této metody je velký hloubkový dosah a zdůraznění projevu té geologické struktury, do níž byla elektroda A uzemněna. Na druhé straně dochází k oslabení projevu struktur ve větší vzdálenosti od proudové elektrody. Pro vyhodnocování je vhodné měřit na témže území při více polohách proudové elektrody. Příklad takového měření je na obr.18, 19. Hodnoty gradientu je nutno přepočíst na úroveň jednotného proudu, obvykle na 1 A. Při měření je velmi důležitým znakem polarita měřených hodnot. Nad vodivou uzemněnou strukturou naměříme křivku sinusového charakteru. Změna polarity udává polohu průmětu hledaného vodiče. Nad neuzemněným vodičem se objevuje pouze zmenšení hodnoty ΔU. U velmi výrazného a širokého vodiče může pokles ΔU jít až k nule.

Metodu nabitého tělesa užíváme všude tam, kde je možno proudovou elektrodu uzemnit do protáhlého objektu situovaného do prostředí o vyšších odporech – např. konec jeskynní chodby s mocnější sedimentární výplní, vývěr nebo ponor.

K obr.18, 19: (Poznámka MK: tyto obrázky neobsahuje ani originál; je možné, že se staly součástí výše uvedeného složeného obr.7.) V jeskyni Malý lesík jsou prostory zaplněny jílovitými sedimenty, jejichž odpor lze odhadnout na 10—30 Ω.m, což je zhruba o dva řády méně než u pevných vápenců. Spojnice míst, kde gradient potenciálu mění polaritu, určuje průběh té vodivé struktury, do které je uzemněna proudová elektroda A. Její průběh sleduje také poloha potenciálu U a směr určuje protažení a zředění izolinií. Ostatní blízké neuzemněné vodivé zóny lze nalézt pomocí zmenšené hodnoty gradientu. Na křivkách potenciálu však často nejsou vůbec zřetelné. Pro ilustraci je poloha vodivých zón všude vyznačena šipkami. Z křivek je patrné, jak pole bodového zdroje se vzdáleností rychle klesá. Takto lze sestrojit průběh průmětu zkrasovění na povrch. Rozlišit výškové úrovně zkrasovění z výsledků měření metodou nabitého tělesa většinou nelze. To však lze zjistit z VES.

 

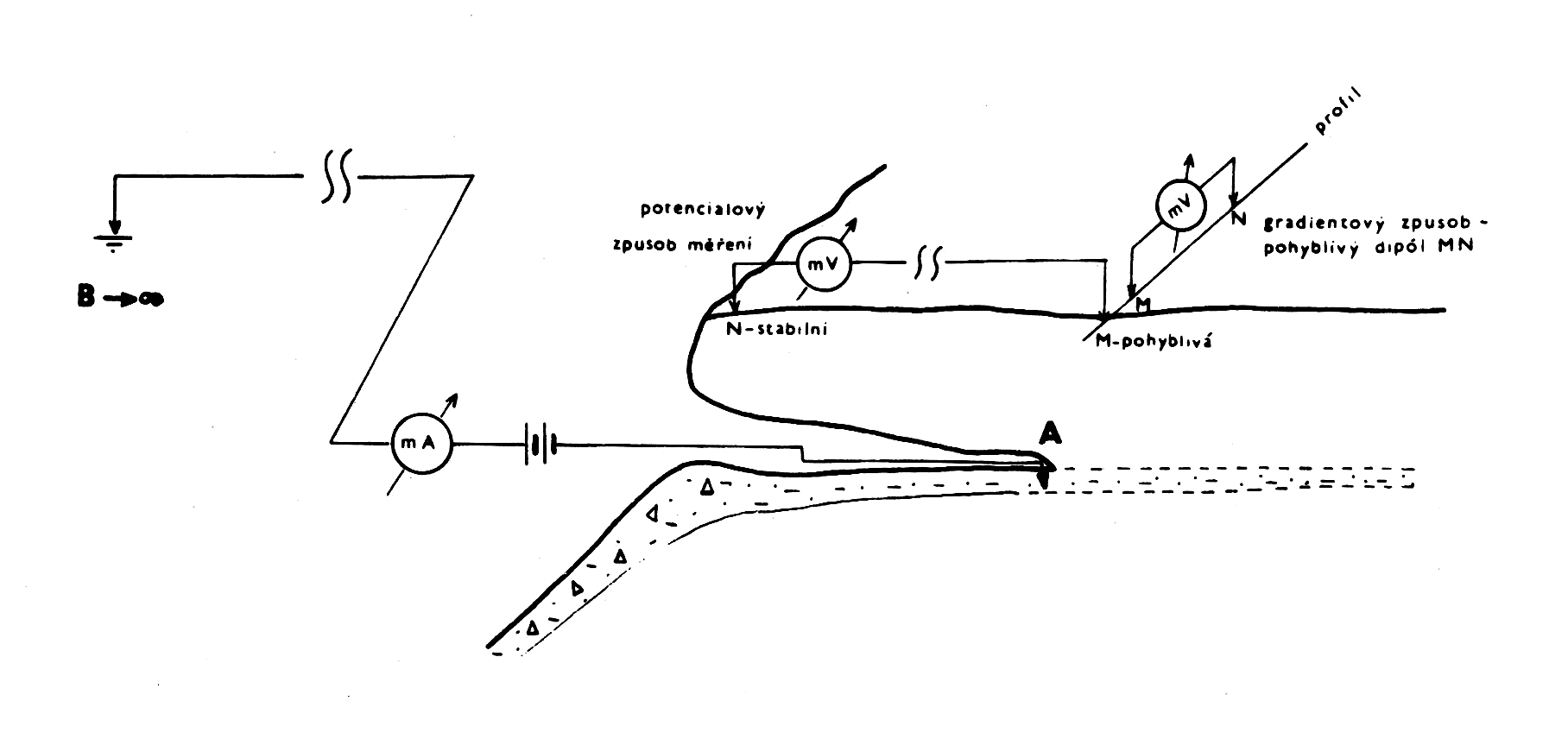
Obr.16: Schéma zapojení v metodě nabitého tělesa.

 

 

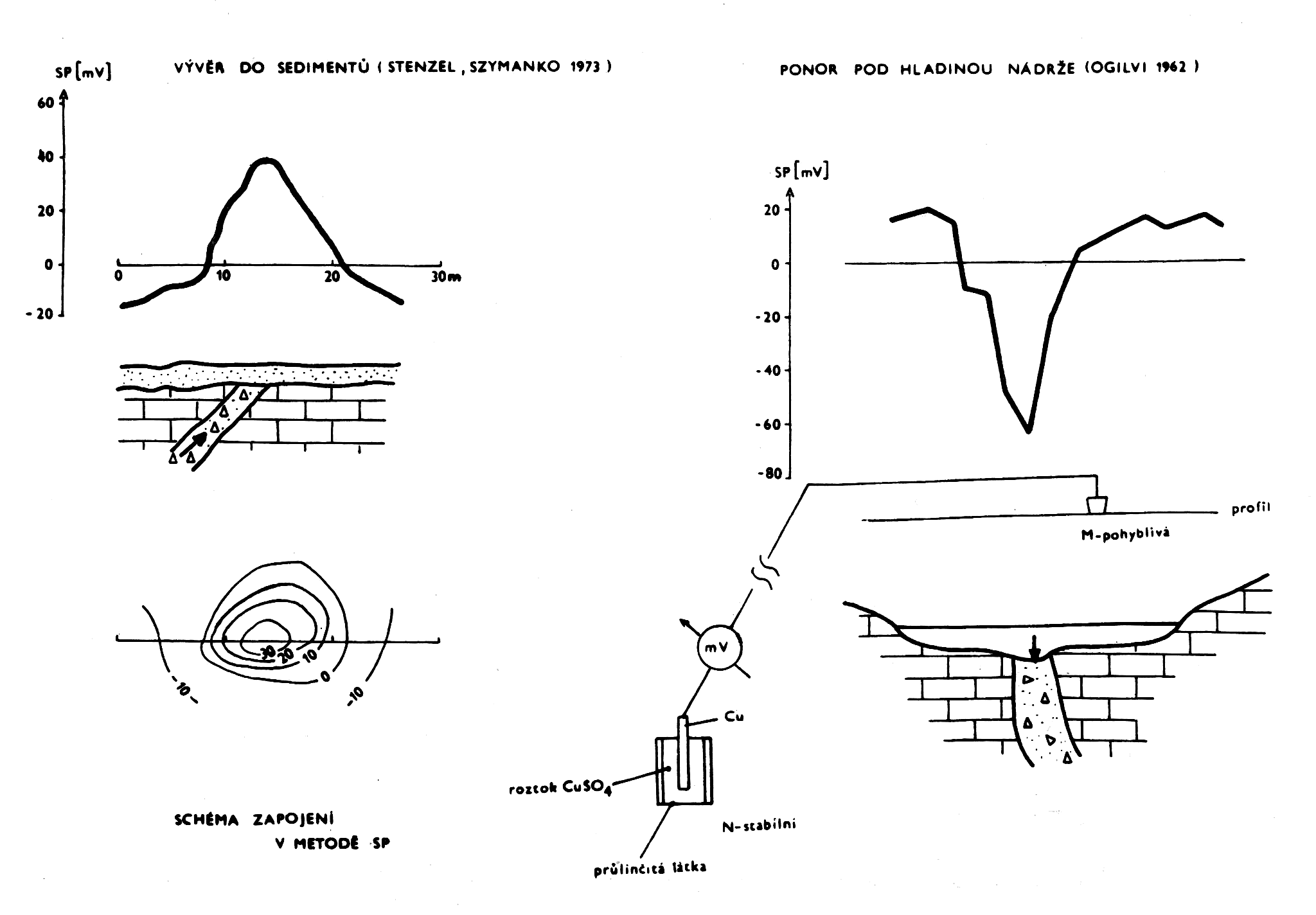
Obr.17: Příklady průběhu pole SP nad poruchovou zónou s pohybem podzemní vody.

 

 

I.A.c) Metody elektrochemické

Z této skupiny metod zde bude zmínka jen o metodě spontánní polarizace (SP) v případě měření přirozených elektrických polí filtračního původu. Při průtoku vody horninovým prostředím, při dostatečné rychlosti a mineralizaci, dochází ve směru toku k vytváření relativně kladného potenciálu oproti těm místům, odkud voda teče. Spád filtračních potenciálů může dosáhnout až 100 mV/km. Jejich měřením je v příznivých případech možno vysledovat směr proudění podzemní vody v sedimentech (zvodněném kolektoru), skryté vývěry a ponory, místa netěsností v přehradní hrázi apod. Z obr.17 je vidět, že místo soustředěného vývěru nebo vtoku podzemní vody se může projevovat lokální anomálií o velikosti do 100 mV. Polarita filtračního elektrického pole určuje směr toku.

Při měření je nutno používat tzv. nepolarizovatelných elektrod, viz schéma zapojení na obr.17b. Elektricky vodivé spojení aparatury s prostředím je v nepolarizovatelných elektrodách realizováno měděnou tyčinkou obklopenou nasyceným roztokem CuSO4 přes porézní nebo průlinčitý obal elektrody – keramika, plsť, hasičská hadice, dřevo. Měří se potenciálovým způsobem. Používá se stejných aparatur jako pro odporová měření.

 

Přístroje pro stejnosměrné metody

Pro měření stejnosměrným proudem se používají tytéž aparatury. U nás jde převážně o různé typy přístrojů řady GESKA, vyrábí je n.p. Geofyzika Brno. Tyto přístroje musí mít při měření napětí vysoký vstupní odpor (desítky až stovky MΩ). Měří proud a napětí nebo přímo odpor. Jsou vybaveny spínačem proudu a kompenzátorem polarizace (odstraňuje rušivá stejnosměrná napětí na měřících elektrodách). Rozsahy měření jsou pro napětí i proud od 1 mV (mA) do 3000 mV (mA) při plné výchylce ručkového měřidla děleného tak, aby bylo možno odečítat setiny plné výchylky.

Základ amatérsky vyrobeného přístroje může tvořit univerzální měřidlo vybavené dostatečně jemným kompenzátorem polarizace s možností přivedení napětí obou polarit zhruba o maximální hodnotě 1 V na vstup přístroje. Měřící a proudový okruh mohou být případně odděleny jako při měření metodou nabitého tělesa.

Pro tyto účely jsou vhodná dvě univerzální měřidla:

Obě měřidla mají při měření napětí zajištěn vstupní odpor 10 MΩ na všech rozsazích; nejcitlivější rozsah mají 200 mV (mA), jsou vybaveny 3,5-místným displejem; napájeny 9 V baterií 6 F 22. Při dostatečně vysokém čtení hodnot ΔU, tak aby chyba měření nepřesahovala 5 % jsou obě použitelná.

 

I.B. Metody elektromagnetické

Velká skupina elektromagnetických metod pracuje se střídavým polem generovaným cívkou, smyčkou, přímkovým uzemněným kabelem nebo anténou. Toto primární generované pole indukuje ve vodivých objektech pole sekundární, které má stejnou frekvenci s primárním, je vůči němu fázově posunuto a skládá se s ním v pole výsledné, které se zpětně detekuje měřícím dipólem (cívkou, smyčkou, anténou).

Výhodou těchto metod je rychlost měření, menší počet pracovníků nutných k obsluze a to, že v některých případech není potřeba vytvářet často pracné galvanické spojení se zemí. Nevýhodou je převážně kvalitativní charakter výsledků, intenzivní rušení umělými vodiči (kabely, el. vedení, konstrukce, ploty, potrubí apod.) a jen omezená možnost vyhledávání objektů, které se projevují jako nevodiče.

 

I.B.1) Metoda velmi dlouhých vln (VDV)

V praktickém použití má mezi ostatními významné místo. Řadíme ji do pasivních nízkofrekvenčních metod (pracovní frekvence jsou 15—20 kHz). Měření je velmi jednoduché, není potřeba kabelů, elektrod a generování vlastního pole, aparaturu obslouží 1 pracovník. Ve vhodných geologických podmínkách poskytuje při řešení některých problémů tolik informací, že ji není nutno doplňovat jinou metodou.

Metoda VDV využívá pole vzdálených navigačních vysílaček pracujících na frekvenci převážně od 15 do 20 kHz. Metoda využívá vzniku vířivých proudů, které spolu s koncentračními proudy vytvářejí nad geologickými vodiči obecně orientované a fázově posunuté sekundární pole. Výsledný vektor je pak elipticky polarizován (jeho průvodič opisuje elipsu). Vzhledem k různé intenzitě primárního signálu (výkon vysílače, vzdálenost, místní podmínky, variace) je vhodné konstruovat přístroj tak, aby měřil veličiny na něm nezávislé. Přístroj naší výroby, EDA (vyrábí n.p. Geofyzika), měří sklon malé poloosy elipsy polarizace (ReHz, v %), a poměr délky obou poloos elipsy polarizace (ImHz, v %).

Dále si popíšeme tvar křivek reálné a imaginární složky měřených tímto přístrojem. Vždy předpokládáme, že směr měření je zleva doprava. V obráceném postupu operátora se naměří stejná křivka obrácené polarity.

Nad samostatnou svislou vodivou zónou tvaru tenké desky v homogenním prostředí bez jiných vlivů naměříme v případě ReHz křivku sinusového tvaru, přičemž inflexní bod je v průmětu nad anomálním tělesem (obr.20). Absolutní hodnoty extrémů, vzdálenost minima a maxima, strmost střední části a rozlehlost anomálie je závislá na poměru vodivosti anomálního tělesa vůči okolí, jeho tvaru, velikosti, orientaci a hloubce. Tvar křivky ImHz bývá složitější a většinou se při interpretaci lokálního vodiče nevyužívá.

Metodou VDV lze také rozeznat odporové kontakty – víceméně svislá odporová rozhraní (obr.21). Podobně se projevují okraje mocné svislé desky nebo stupně. Kdybychom mocnou vodivou desku, což jsou vlastně dva blízké odporové kontakty, postupně zužovali na lokální tenký vodič, dostali bychom zase indikaci sinusového charakteru. Podle toho si lze při interpretaci kontaktu zapamatovat, která strana kontaktu má vyšší a která nižší odpory (srovnej obr.21 a 23). Pro rozeznání kontaktu může pomoci průběh křivky ImHz, který v tomto případě mívá charakteristický tvar s dílčím extrémem.

 

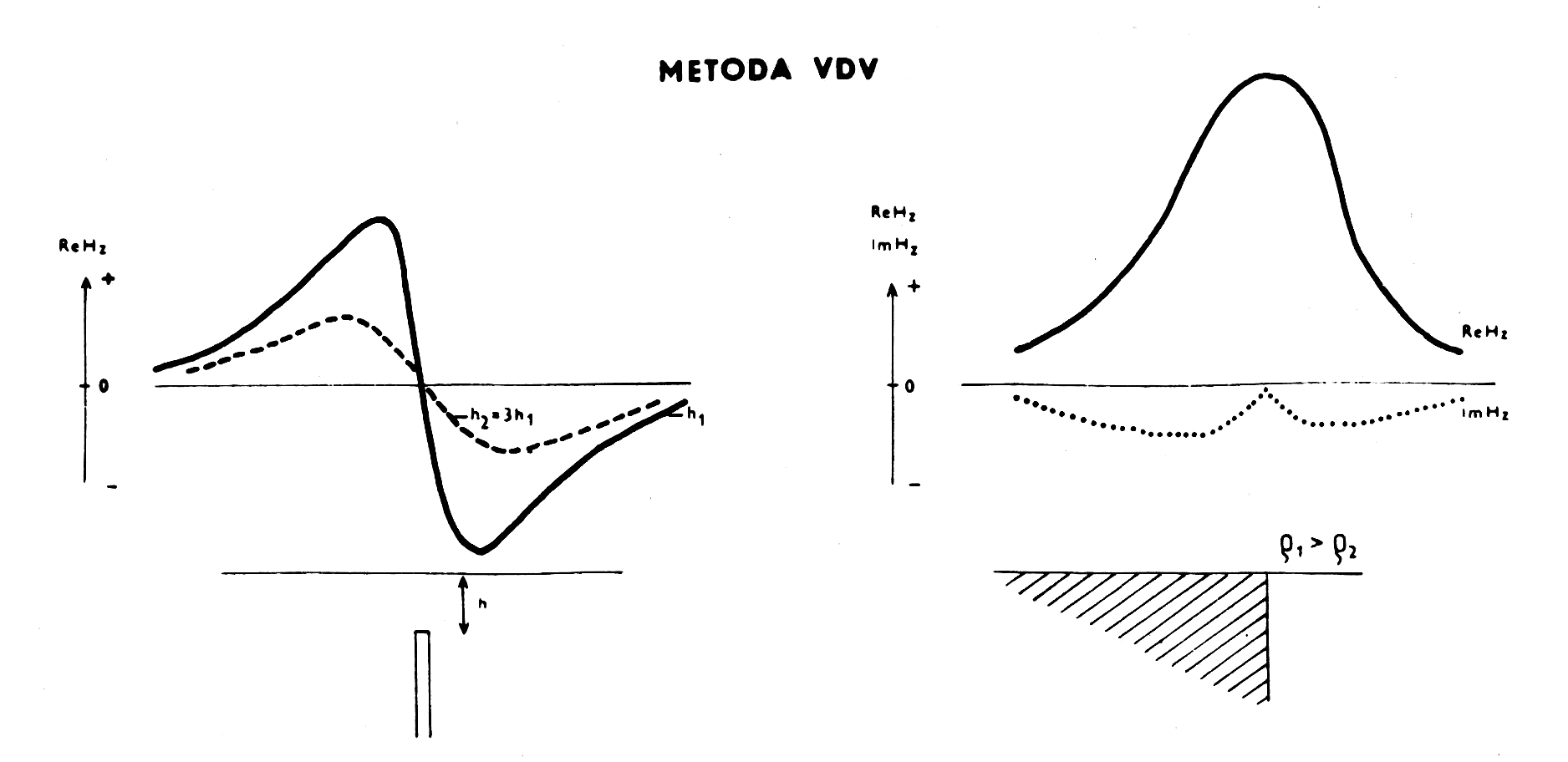
Obr.20 a 21:
20 – vlevo: Charakter křivky ReHz nad vodičem v různé hloubce;
21 – vpravo: Tvar obou křivek nad odporovým kontaktem.

 

 

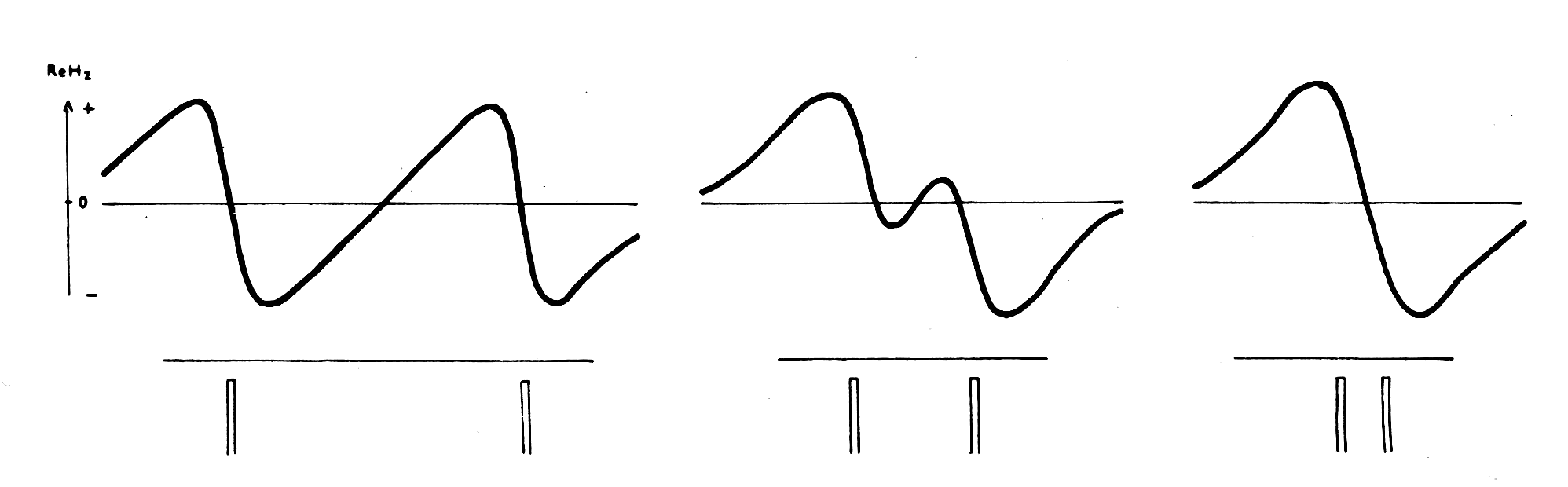
Obr.22: Metoda VDV – tvar křivky ReHz nad dvěma blízkými vodiči.

 

 

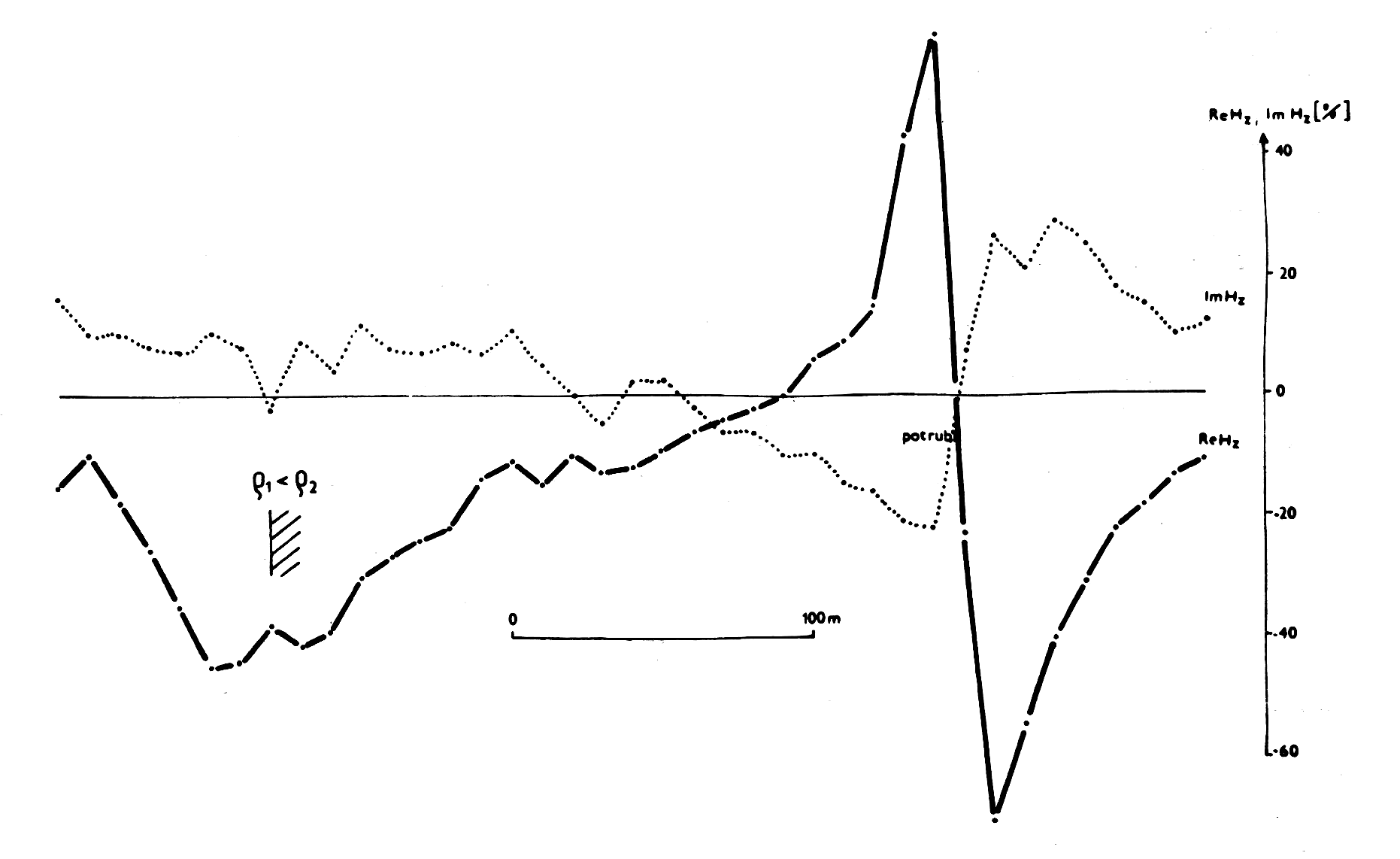
Obr.23: Metoda VDV – ukázka měření nad odporovým kontaktem a umělým vodičem.

 

 

Metoda VDV je velmi citlivá na tvar reliéfu terénu. Je-li měření vedeno kolmo přes údolí a hřeben, naměříme na hřebeni indikaci vodiče a nad údolím nevodiče (obr.8). Rozsah a velikost těchto anomálií jsou úměrné frekvenci výskytu hřbetů a údolí v průběhu profilu a na délce a sklonu svahů. Posunují křivku mimo nulovou hodnotu, takže interpretátor nikdy nevyhodnocuje čisté anomálie způsobené hledanými objekty. Zkušenému pracovníkovi to ale nečiní potíže. Podobně jako všechny elektromagnetické metody je i tato velmi citlivá na umělé vodiče. Jejich projevy jsou velmi ostré a anomálie mají vysoké hodnoty. Také projevy těchto objektů lze snadno rozpoznat a vyloučit. Potíž je v tom, že ještě dosti daleko od nich bývá projev přirozených nehomogenit zastřen.

Výsledky metody VDV mají kvalitativní charakter – lze určit jen polohu vodivých zón a kontaktů, neposkytují informace o číselné hodnotě elektrických odporů. Výsledky se podobají výsledkům odporového profilování a do značné míry je nahrazují. Nelze však volit hloubkový dosah měření. Velkou výhodou je, že na více stanicích lze provést směrovou analýzu nalezených indikací, bez níž by ve složitějším systému, např. tří tektonických směrů, byla interpretace výsledků odporového měření značně obtížná. Sekundární pole totiž vzniká nad lokálním vodičem v největší míře tehdy, je-li vodič orientován směrem k použitému vysílači. Odchylka od tohoto směru nemá přesahovat ±30°. Tato skutečnost je důležitá především pro projektování směru geofyzikálních profilů, na nichž bude měření uskutečněno, a pro volbu stanic. Existence, intenzita či absence anomálie v závislosti na směru stanice umožňuje provedení směrové analýzy zjištěných indikací (obr.24).

 

Obr.24: Měření metodou VDV na profilu 56 na třech stanicích 1,5 km j. Černé Hory.

 

 

Nevýhodu kvalitativní povahy výsledků odstraňuje odporový přístavek ERA, pomocí něhož měříme impedanci Ex/Hy, kterou označujeme ϱVDV, a fázový posun Δφ. Velikost fázového posunu určuje odporový sled prostředí v rámci hloubkového dosahu. Je-li Δφ > 45°, pak ϱ1 > ϱ2 a obráceně. Nad homogenním poloprostorem je Δφ ≈ 45°. Z parametrů ϱVDV a Δφ lze ve výjimečně příznivých podmínkách navíc interpretovat hloubku odporového dvouvrstevného prostředí a hodnotu odporů obou vrstev jakoby šlo o VES (např. mocnost zvětralin, sprašového pokryvu apod.).

 

I.B.2) Elektromagnetické prosvěcování

Řadíme do vysokofrekvenčních aktivních metod – primární pole si sami generujeme. Sovětské aparatury řady SRP užívají frekvencí od 100 kHz do 100 MHz. Tím se zajišťuje rozdílná pronikavost vln prostředím. Šířené pole je do značné míry přímočaré a podléhá zákonům vlnové optiky. Principem metody je sledování útlumu vln v souvislosti s elektrickým odporem prostředí. Vodivé objekty (rudní tělesa, jeskynní sedimenty) jsou místy zvýšeného útlumu, nevodivé horniny (nezkrasovělý vápenec, dutina) pole snáze propouštějí.

Na obrázku 25 je ideový příklad při měření v důlních dílech při rudní prospekci. Měřením při více polohách vysílače lze ohraničit pravděpodobný tvar a polohu vodivého rudního tělesa. K útlumu vln za tělesem dochází tehdy, je-li jeho příčný rozměr větší než ½ délky vlny (při frekvenci 30 MHz je délka vlny λ = 10 m).

 

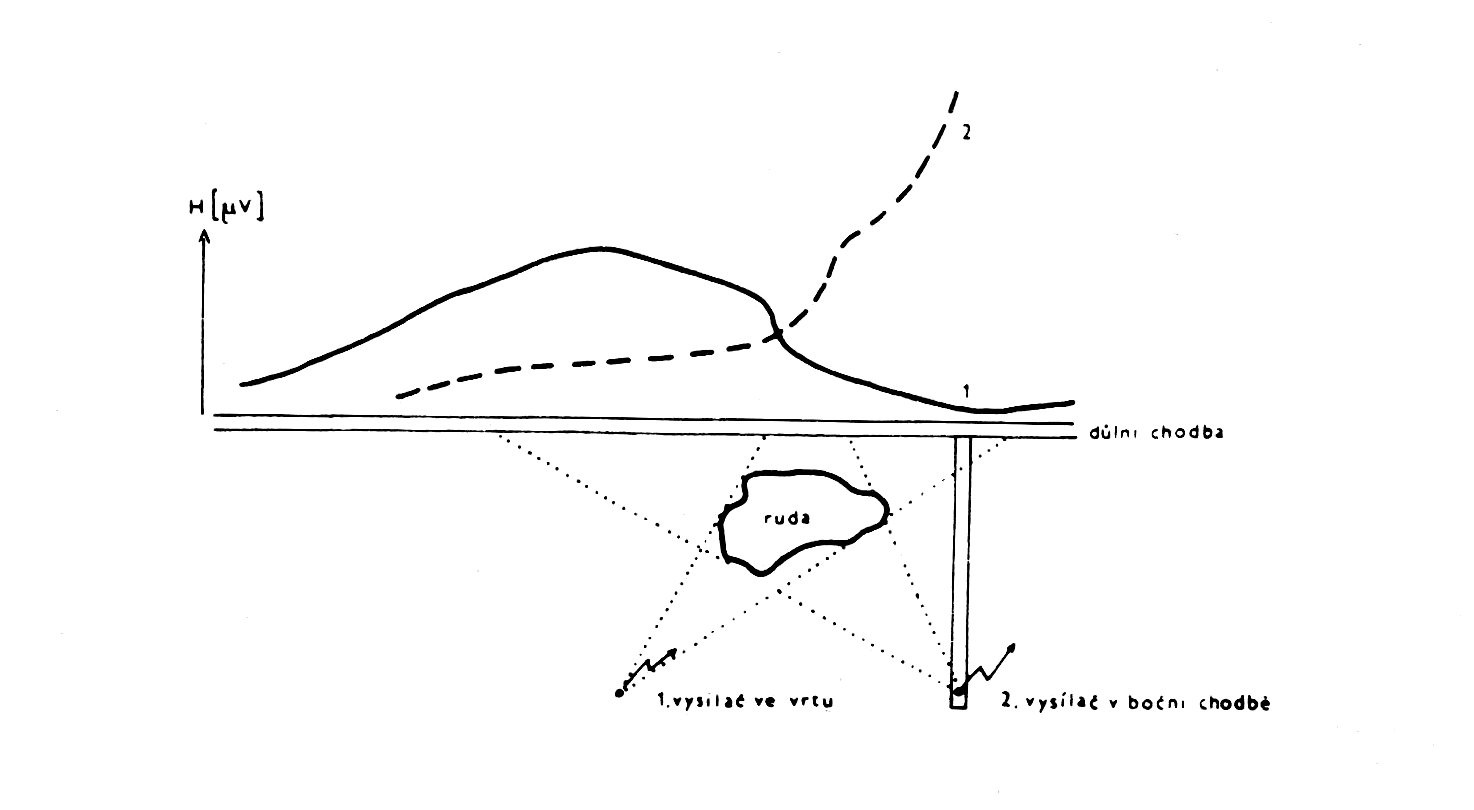
Obr.25: Ideový příklad použití elektromagnetického prosvěcování.

 

 

Ve speleologické praxi se pro vyhledávání předpokládaného směru pokračování dutin používají běžné kapesní vysílačky. Pro amatérské vysílání je státními orgány vyhrazeno frekvenční pásmo 3 MHz, pro účely organizací pak okolo 30 a 80 MHz. Pro náš účel jsou vhodné první dvě frekvence.

Vzdálenost, na níž dojde k útlumu pole e-krát (2, 7×), je dána vztahem:

 

 

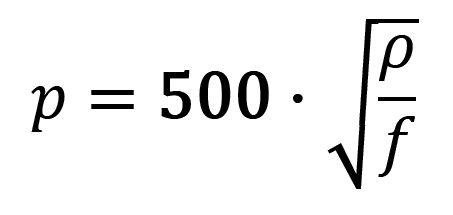
Pro ϱ = 3000 Ω.m a f = 3 MHz je to 16 m, při f = 30 MHz už 5 m. Prostupnost vlny je tedy při vyšších frekvencích a nižších odporech poměrně malá. Zvláště při malých výkonech dostupných vysílaček by nemělo docházet k navázání spojení už při průchodu horninovým prostředím na vzdálenost několika desítek m. Pracovníci oddělení pro výzkum krasu při Moravském muzeu v Brně uvádějí, že navázali spojení na vzdálenost více než 100 m, vymezili „oblast slyšitelnosti“ o velikosti asi 25×4 m, a na povrchu tak vysledovali výchoz zkrasovělé pukliny o směru 120°, podle níž došlo k vytvoření komínovitých prostorů Zadní kaple v Ochozské jeskyni (Burkhardt, Nesrsta 1970).

Vhodnější způsob než vyhledávat „oblasti slyšitelnosti“ je vybavit přijímač měřidlem intenzity přijímaného signálu. Pak je možno výsledky v ploše nad jeskyní zobrazit ve formě mapy izolinií měřeného pole, která dává mnohem podrobnější obraz o poloze a tvaru minim a maxim. Maxima signálu mívají většinou úzké protáhlé tvary, které z větší části sledují směr zkrasovělých puklin a odpovídají jejich vyústění na povrch. Schéma měřiče intenzity signálu k běžným vysílačkám je publikováno ve Slovenském krasu (Burkhardt, Gregor 1974).

 

 

 

II. GRAVIMETRIE

V každém místě zemského povrchu působí gravitační zrychlení (tíže), které je vektorovým součtem především přitažlivosti zemského tělesa a odstředivé síly rotující Země. V menší míře se uplatňují gravitační účinky Měsíce (2 μm.s−2) a Slunce (1 μm.s−2).

Aproximujeme-li tvar Země rotačním elipsoidem, je možno pomocí Helmertova vzorce vypočíst normální tíži g v libovolném bodě zemského povrchu.

 

 

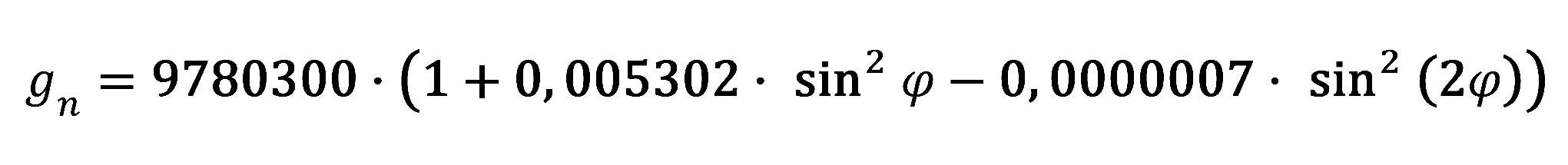
kde:

Takováto tíže by měla být za předpokladu hustotně homogenní Země při hladině moře na povrchu tohoto elipsoidu. Hodnoty gn jsou tabelovány.

Účelem tíhových měření je ale zjistit anomální tíži Δg. Dostaneme ji odečtením normální tíže a účinku všech hmot nad hladinou moře od hodnoty tíže g v daném bodě naměřené a zavedením opravy na účinek všech hmot v bližším okolí měřeného bodu, pod i nad jeho úrovní. Takovouto anomální tíži nazýváme Bouguerovou anomálií:

 

 

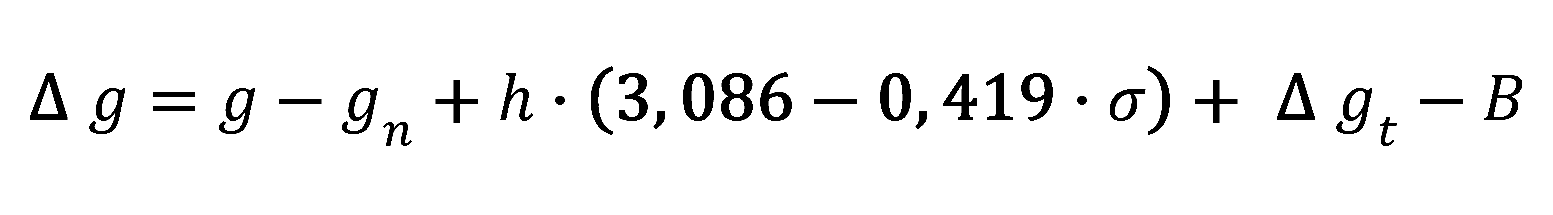
kde:

Hodnota měřené, normální i anomální tíže se udává v μm.s−2, hustoty v kg.m−3. Hodnota Δg se vztahuje buď k nějaké statisticky určené relativní hodnotě nebo se přepočítává na absolutní hodnoty tíže po připojení tíhového pořadu na státní tíhovou síť.

Vlastní interpretace se provádí buď studiem tvaru úplných Bouguerových anomálií nebo studiem transformovaných tíhových polí – vyseparovaných reziduálních anomálií, polí analyticky transformovaných na jiné výškové úrovně, různých derivací tíže.

Pro účely průzkumu jeskyní nás zajímají pouze lokální anomálie a to většinou anomálie z malé hloubky. Vždy není nezbytně nutné zavádět normální tíži a korekce do větších vzdáleností od měřeného bodu. Někdy stačí hodnoty opravit jen o chod přístroje a nadmořskou výšku. To si můžeme někdy dovolit při husté síti tíhových bodů na malé ploše a rovinném, byť i šikmém povrchu.

Se zvětšováním hustoty měření lze vyčleňovat stále drobnější anomálie, které jsou převážně odezvou mělkých hustotních nehomogenit. V tíhovém poli jsou totiž zaneseny vlivy všech nehomogenit, od těch nejhlubších až po nerovnosti terénu.

Například pro nalezení vyústění krasového komínu je někdy třeba zahustit měření až na síť 1×1 m. Pro tyto účely je nutno měřit s vysokou přesností na hranici citlivosti přístroje a v natolik husté síti bodů, aby anomálie byla zachycena alespoň třemi body kvůli vyloučení nahodilých chyb.

Na obr.9 je příklad reziduální anomálie nad jeskyní Kůlnou. Blízká prostorná dutina vyvolává anomálii −4 μm.s−2. Zkrasovění Sloupských jeskyní se v tíži neprojevuje. V geoelektrice je ovšem zřetelné. Dnešní gravimetry měří s přesností okolo ±0,2 μm.s−2.

 

Tabulka 3. Maximální projev horizontálního nekonečného válce (v závorce koule) v různých hloubkách o diferenční hustotě 2600 kg.m−3, který představuje jeskynní chodbu (resp. dómovitou prostoru):

Hloubka středu válce (koule) Velikost projevu válce / koule o poloměru
r=1 m r=3 m r=5 m
2 m 0,54 (0,18) — —
3 m 0,36 (0,08) — —
5 m 0,21 (0,03) 1,96 (0,78) —
10 m 0,11 0,98 (0,20) 2,72 (0,9)
20 m 0,05 0,49 (0,05) 1,36 (0,23)
50 m 0,02 0,20 0,54 (0,04)
100 m 0,01 0,10 0,27

 

Tíhové anomálie jsou odezvou nerovnoměrností v rozložení hmoty. Prázdná prostora je extrémním případem tělesa s hustotou σ=0. Každé porušení a podrcení horniny, navětrání, zvýšená pórovitost a vodonasycenost vedou ke snížení hustoty hornin. Nezpevněné sedimenty (štěrky, písky, jíly) mají v důsledku vyšší pórovitosti nižší hustoty. V gravimetrii jsou důležité hustoty hornin v přirozeném stavu. Zkrasovění se projevuje vždy úbytkem hmoty, tedy zápornými gravimetrickými anomáliemi – tíhovými minimy. Hustoty vápenců jsou především v důsledku dolomitizace značně variabilní.

 

Tabulka 4. Hustoty některých hornin (Mareš a kol. 1979):

Hornina Hustota [g.cm−3]
Sypké zeminy 1,4—1,9
Pískovce 2,2—2,75
Vápence, dolomity 1,8—3,0
Žuly 2,4—2,8
Gabra 2,8—3,0
Čediče, diabasy 2,5—3,15

 

Na obr.26 je příklad projevu Mladečských jeskyní v mapě izolinií úplných Bouguerových anomálií. K JJZ klesající tíhové pole je utvářené nehomogenitami regionálního charakteru. V tomto poli se jeskyně projevují lokálním tíhovým minimem, které se s regionálním polem sčítá a způsobuje lokální vyklenutí izolinií. Po odstranění regionálního pole by zůstala oválná reziduální anomálie směru SV—JZ o minimu asi 1,5 μm.s−2. Podle tohoto měření je naděje na objevení neznámých prostor především v s. a sz. části území.

 

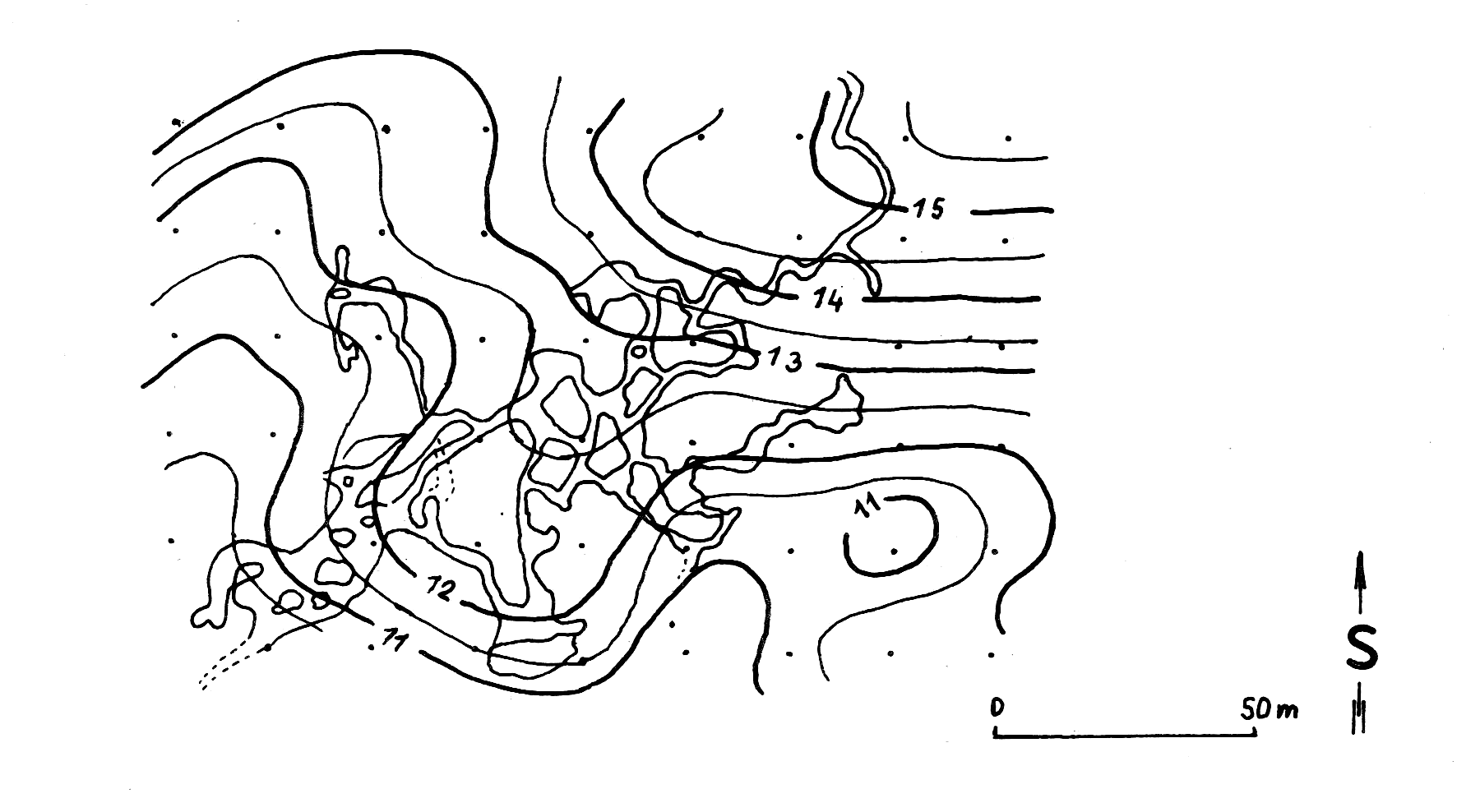
Obr.26: Mapa úplných Bouguerových anomálií [μm.s−2] nad Mladečskými jeskyněmi s vyznačením půdorysu jeskyní a polohy tíhových bodů v síti 20×20 m (Tomek 1975).

 

 

 

III. GEOTERMIKA

Zhruba od hloubky 20—30 m níže teplota Země stále stoupá. Vysoké teploty zemského nitra se dávají do souvislosti především s radioaktivním teplem způsobeným rozpady, v menší míře souvisí s teplem gravitačním a zbytkovým. Teplotní variace v důsledku střídání ročních období se projevují právě do těch 20—30 m podle tepelné vodivosti hornin a zejména v souvislosti s přítomností či absencí vegetačního pokryvu, který je významným tepelným izolátorem. V této hloubce se udržuje průměrná roční teplota. U nás většinou 7—9 °C. Denní teplotní variace se už většinou pod hloubkou 1 m neprojevují.

Termometrie je jednou z přímých metod, které mohou vést k vyhledávání dutin. V mělce pod povrchem uložené prostoře, která je dostatečně vertikálně rozsáhlá, a která svým stropem zasahuje do vrstvy s výraznou změnou teplot v důsledku ročních teplotních změn, dochází v zimním období díky cirkulaci vzduchu k prohřívání stropu. Vzduch v takovém případě cirkuluje i v úplně uzavřené prostoře jen díky tomu, že spodní část prostory je teplejší nežli strop. Termometrie v té nejprimitivnější formě je speleologům dávno známa jako hledání tzv. „mastných fleků“ – míst s roztopeným sněhem nebo jinovatkou. Je zřejmé, že teplotní měření je nejlépe provádět tehdy, když dochází k největšímu teplotnímu rozdílu mezi hledaným objektem a okolím. Nevýhodou termometrických prací je možnost odstranit projev denních variací a projev rozdílného teplotně izolačního vlivu pokryvu, což se dělá měřením v 1,5—2 m hlubokých děrách. Právě v krasu není většinou možno tak hluboké díry dělat vpichovkou, je nutno je navrtávat a to představuje dosti vážný technický problém. Při měření je nutno během dne provádět v jedné díře kontrolní měření. Pokud nejsou všechny díry přesně stejně hluboké, je nutno si kvůli opravám změřit závislost teploty na hloubce.

Podobně jako dutinu lze hledat polohu soustředěného vývěru ze skály do sutě a svahovin. Teplotní měření společně se sledováním pole filtračních potenciálů může dát v případě nevelkých mocností pokryvu pěkné výsledky. Polohu zakrytého vývěru je možno na rozdíl od dutiny hledat i v parném létě v době nejhlubšího prohřátí povrchové vrstvy.

Termometrií lze také vyhledávat skryté vývěry, které se v náplavech rozptylují a přímo přes štěrky dotují povrchový vodní tok. V takovém případě měříme teplotu u dna vodního toku a práce je mnohem efektivnější než při měření v děrách. U menších vodních toků se doporučuje v každém místě měřit poblíž obou břehů a uprostřed. Z toho lze někdy usoudit, na které straně vodního toku k vyvěrání dochází. Pro tato měření se nejlépe hodí nejparnější léto a současně doba nejnižšího vodního stavu. Rovněž v zimě bývají dostatečné teplotní kontrasty, ale měření bývá ztíženo ledovým krunýřem. Příklad takového měření podél toku Říčky v jižní části Moravského krasu je na obr.27. Zde je výsek dvojího měření z ledna a srpna 1985. I když v srpnu bylo měřeno za vysokého vodního stavu, přesto se v obou případech objevuje na metráži 8,6 indikace skrytého vývěru do říčních náplavů z levé strany údolí. Na srpnovém měření je vidět porušení teplotního stavu toku rybníčkem, který na větší vzdálenost způsobuje variabilitu teplot.

 

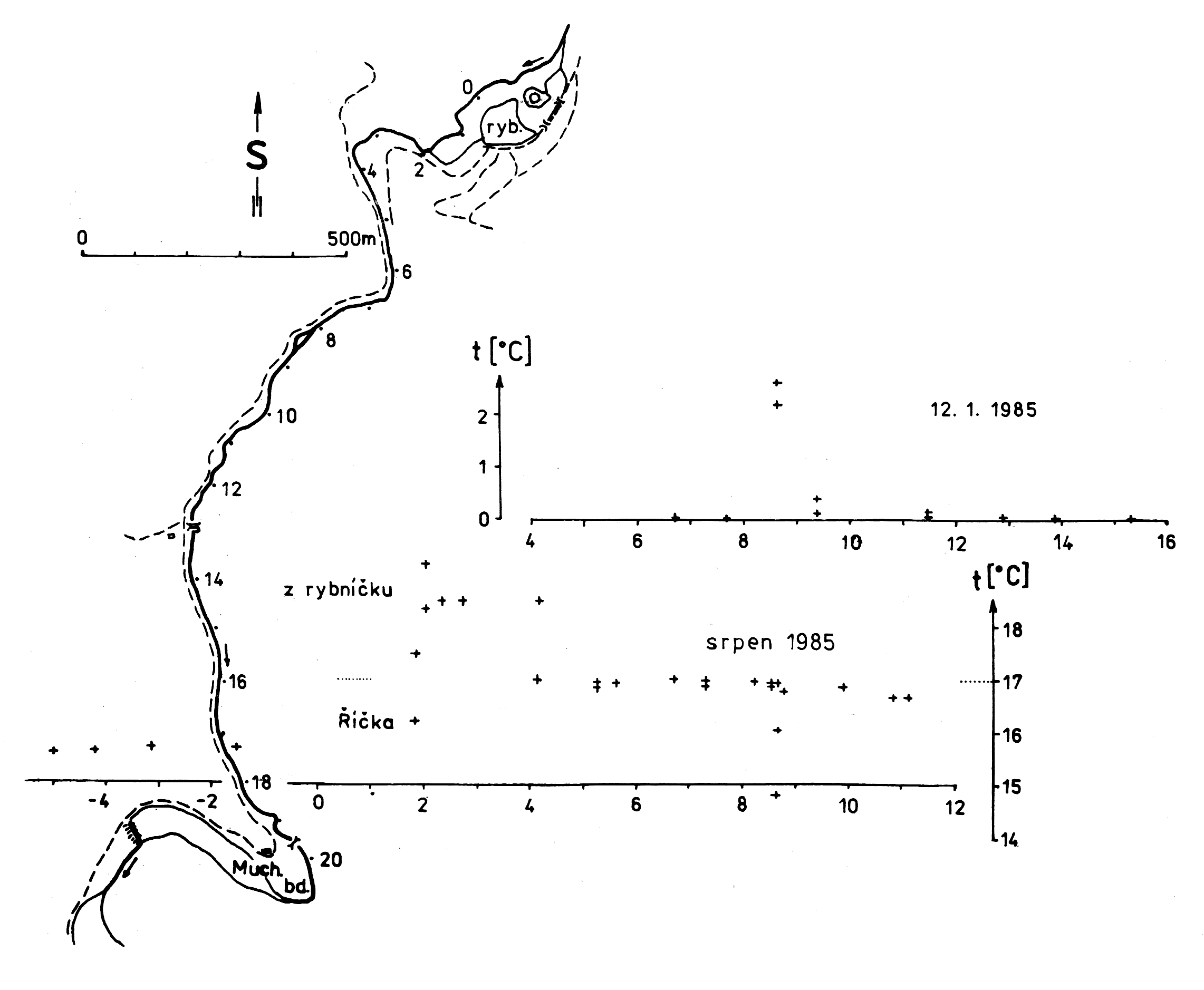
Obr.27: Příklad měření teploty vody u dna vodního toku. Říčka v jižní části Moravského krasu mezi Muchovou boudou a rybníčkem asi 800 m pod Bělkovým mlýnem.

 

Mnohem efektivnější je snímkování na materiál citlivý na tepelné záření nebo snímkování tepelného záření detektory. Pro tyto účely se v infračervené oblasti využívají dvě okna, pro která je atmosféra propustnější (pásma vlnových délek 3—5 μm a 8—14 μm). Snímkování se osvědčuje v oblastech se sporou vegetací (stepi, pouště). V důsledku rozdílu teploty bývají takto v příbřežních krasových oblastech snadno zjistitelné vývěry sladké vody do moře.

 

 

 

IV. SEISMICKÉ METODY (SEISMIKA)

Seismické metody představují soubor geofyzikálních metod zkoumání svrchních partií zemské kůry založených na studiu uměle vyvolaných elastických vln. Hlavním zdrojem elastické energie je odpal trhavin při průzkumu mělčích partií; lze však použít i úderu kladiva, dopadu závaží na podložku apod. Seismický průzkum má největší význam pro vyhledávání a upřesňování ložisek plynných a kapalných kaustobiolitů (ropa, plyn) a pro řešení různých strukturně-geologických úkolů; lze jej však užít i pro řešení rozmanitých inženýrsko-geologických a hydrogeologických úkolů.

Při studiu a řešení většiny problémů mají obzvláštní význam ty vlny, které se od zkoumaného objektu vracejí zpět k povrchu země, tj. vlny přímé, odražené a čelné.

Uvažme v další situaci pod povrchem země dle obrázku 28. R je horizontální rozhraní oddělující vrstvu z1 od podložního poloprostoru z2. Obě vrstvy jsou charakterizovány rychlostmi šíření vln (v1, v2) a hustotami (ϱ1, ϱ2).

 

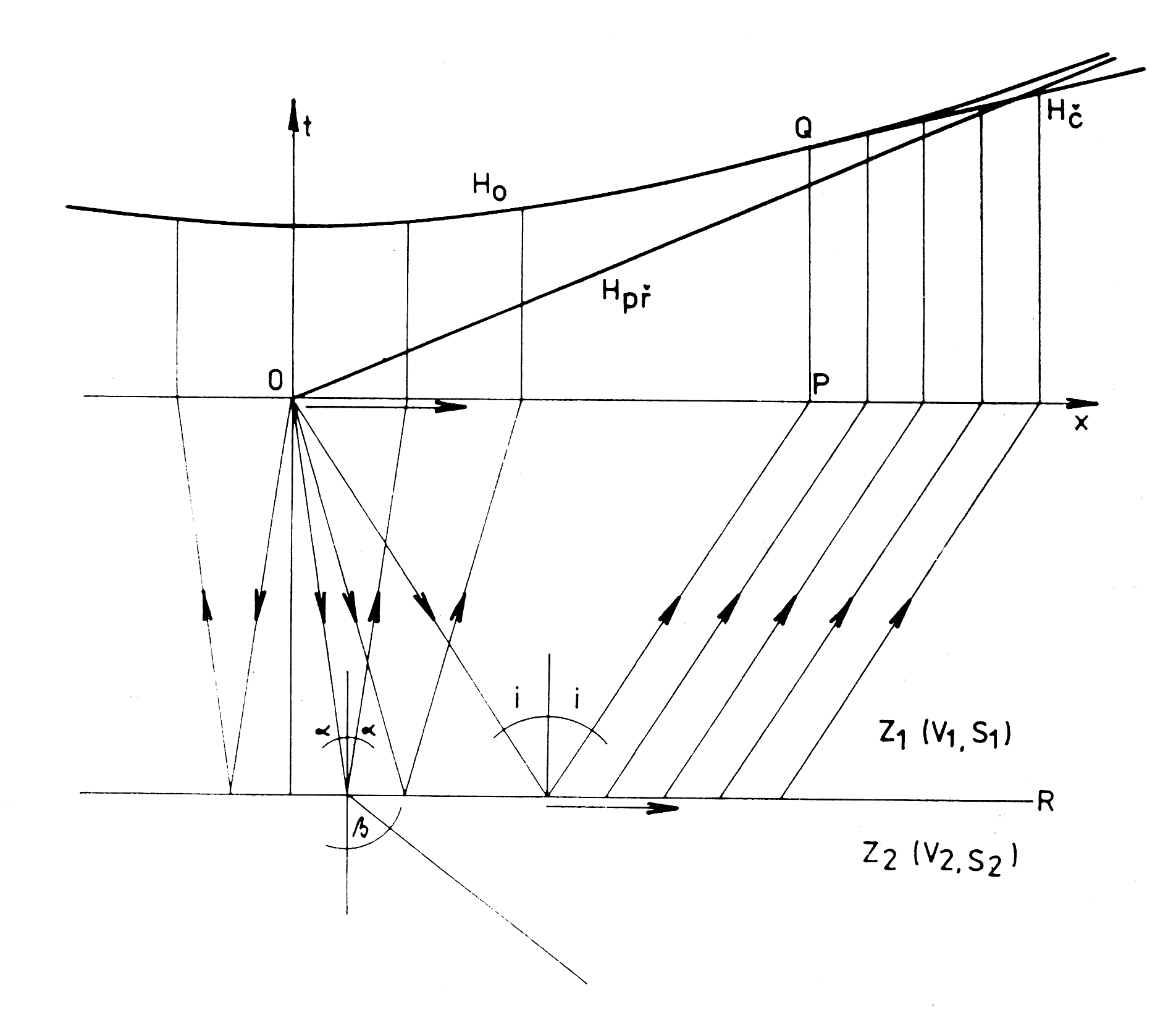
Obr.28: Schéma vzniku a hodochrony seismických vln.

 

 

Seismická energie vyvolaná v bodě výbuchu O se šíří ve vrstvě z1 rychlostí v1 jako přímá vlna. Po dopadu na rozhraní R vznikají v bodě dopadu dvě druhotné vlny – odražená a lomená. Vlna odražená se vrací k zemskému povrchu rychlostí v1 pod stejným odrazovým úhlem α; vlna lomená klouže podél rozhraní R a šíří se spodní vrstvou z2 rychlostí v2. Protože v2 bývá větší než v1, vlna lomená předbíhá vlnu přímou. Při postupu podél rozhraní vyvolává lomená vlna v nadložní vrstvě z1 kmitání částic – do prostředí z1 se šíří tzv. čelná vlna pod kritickým úhlem i.

Podle Snelliova zákona platí:

 

 

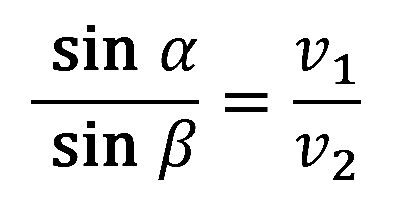
jestliže β = 90°, pak sin β = 1 a sin α = sin i = v1 / v2.

Vidíme tedy, že sinus kritického úhlu i je dán poměrem rychlostí horní a spodní vrstvy.

Jak je patrné z obrázku 28, bod P, k němuž přichází paprsek čelné vlny pod kritickým úhlem i, lze definovat jako počáteční bod čelní vlny. Za tímto bodem odražené vlny přicházejí k zemskému povrchu později než vlny čelné a lze proto je špatně registrovat.

Seismický profil lze tedy pro zadaný bod výbuchu rozdělit na dva úseky – okolí bodu výbuchu, kde obvykle sledujeme vlny odražené, a oblast vzdálenější, kde registrujeme vlny čelně (lomené). Sestavíme-li grafy závislostí času příchodu vln (t) na vzdálenosti (x), dostaneme tzv. hodochrony. Tak na obrázku 28 jsou Hpř, Ho a Hč postupně hodochrony vln přímých, odražených a čelných.

Rychlosti seismických vln v horninách záleží na charakteru horniny (horniny sedimentární, vyvřelé, metamorfované) a také na podmínkách vzniku, vývoje a uložení těchto hornin. Ve vlastní hornině jako celku rychlosti záleží na rychlostech šíření seismických vln v pevných částech horniny (skeletu), na porózitě (% objem pórů v hornině) a také na rychlostech ve výplních pórů. Přitom platí, že rychlosti v horninách s vysokou porózitou jsou menší než při nízké porózitě, podobně jako ve zvodnělých horninách jsou rychlosti šíření vln větší než v horninách nezvodněných. U pevných částí hornin rychlosti záleží na mineralogickém složení, u výplní pórů pak na charakteru této výplně (vzduch, voda, plyn, ropa – důležité při přímém vyhledávání ložisek uhlovodíků). Významný je tlak, kterému byly nebo jsou horniny vystaveny; zvýšení tlaku vede ke snížení porózity, a tím i ke zvýšení rychlosti. Při zemském povrchu, kde jsou horniny často vystaveny intenzivnímu zvětrávání, jsou rychlosti seismických vln výrazně nižší než při hlubším uložení. Obecně lze říci, že rychlosti vln ve starších horninách (např. prvohorní devonské vápence) jsou obvykle vyšší než v horninách mladších (např. třetihorních). U výše popsaných podélných vln přímých, odražených a čelných (lomených) rychlosti stoupají od hodnot 200—1000 m.s−1 (přímé povrchové vlny – navětralá půdní vrstva, písek, štěrk, hlíny) až po 6000—7000 m.s−1 (vápence, dolomity, vyvřelé a metamorfované horniny ve větších hloubkách).

 

K zemskému povrchu mohou při seismickém průzkumu přicházet ještě další typy vln:

 

Příčné vlny (odražené a čelné)

Kromě doposud popisovaných vln podélných, charakterizovaných zónami nahuštění a zředění prostředí (deformace objemové), existují vlny příčné, vázané na tvarové (střižné) deformace; zde dochází k posunům kolmým na směr šíření vlny. Rychlost šíření těchto vln je oproti vlnám podélným menší; nešíří se také v kapalinách a plynech.

Vlny transformované

Po dopadu např. podélné vlny na rozhraní může vzniknout i jedna vlna podélná a dvě příčné – horizontálně a vertikálně polarizované.

Násobné odrazy

Vznikají zpětným odrazem vln od zemského povrchu (nebo od některého rozhraní uvnitř zkoumaného geologického profilu), novým návratem do hloubky a dalším odrazem a návratem k povrchu.

Mikroseismy

Tj. záznam nepravidelných pohybů půdy, způsobených různými vlivy (povětrnostní podmínky – vítr, déšť, vliv dopravy, zemědělských strojů).

 

Všechny tyto typy vln obvykle působí rušivě na příjem užitečného signálu, a je třeba, aby byly při terénním měření i při následném souhrnném zpracování potlačovány. Pro spolehlivé zpracování je třeba, aby poměr užitečného signálu k šumu byl alespoň 1,5:1.

 

Registrace a zpracování seismického signálu

Při provádění terénních měření se obvykle postupuje po vytýčených profilech, projektovaných pro řešení zadaného geologického úkolu. Po odpalu trhaviny ve vyhloubených vrtech (nebo po úderu kladiva, dopadu závaží apod.) vznikají seismické vlny, které se šíří zemí, odrážejí se a lomí na rozhraních a postupují zpět k zemskému povrchu. Zde působí pohyb půdních částic – jejich mechanická energie je pak přeměňována na elektrický signál pomocí geofonů (obvykle indukčních – při příchodu seismické vlny se rozkmitá plášť geofonu s magnetem, zatímco setrvačná hmota cívky se snaží zůstat v klidu. Relativním pohybem cívky v magnetickém poli vzniká elektromotorické napětí). Elektrický signál je veden dále do zesilovačů (zesílení signálu tak, aby mohl být čitelně registrován; frekvenční filtrace – pro zesílení užitečných a potlačení nežádoucích druhů vln – a regulace amplitudy seismického signálu, tj. největší výchylky částice z rovnovážné polohy) a do registračního zařízení, kde je zaznamenán buď ve formě definitivního (nereprodukovatelného) nebo prozatímního (reprodukovatelného) zápisu. Definitivního zápisu lze použít k přímému zpracování seismických měření, naproti tomu prozatímní zápis (obvykle na magnetofonové pásce, v analogové nebo digitální formě) bývá dále zpracováván ve vyhodnocovacím středisku. Konečným produktem je seismický záznam (např. při oscilografické reprodukci) nebo časový či hloubkový řez (plošný záznam výsledků měření na příslušném profilu v časové nebo hloubkové formě). Řezy se dále plošně zpracovávají s návazností na další geologické a jiné údaje, výsledky vrtů atd. a konstruují se strukturní mapy zájmového horizontu (např. pro rozhraní mezi neogénem a jeho podložím).

Pro úplnost ještě poznamenáváme, že zatímco při tzv. velké seismice (řešení strukturních, naftově-geologických, regionálně geologických a jiných problémů) bývají zdroje vlnění a registrující geofony ve větších vzájemných vzdálenostech (desítky až stovky metrů), při inženýrsko-geologických, hydrogeologických a jiných studiích, včetně aplikací na území krasovém a při vyhledávání podzemních dutin, bývají tyto vzdálenosti sníženy – body registrace často až na 1 m, zdroje vlnění pak až na 12 m. K registraci je užíváno 48 až 24-kanálových aparatur (např. aparatura TRIO), často však postačí malé přenosné aparatury (1-kanálová aparatura BISON).

Vyhledávání podpovrchových dutin povrchovým seismickým měřením (v n.p. GEOFYZIKA Brno od roku 1966) je založeno na faktu, že seismické vlny šířící se homogenním (stejnorodým) prostředím mají přesně definovatelný útlum. Vyskytuje-li se nějaká překážka (nehomogenita), způsobí změnu amplitudy; dobré indikace dává tedy povrchová registrace amplitud čelní vlny, vznikající na seismickém rozhraní v podloží dutiny. Čím menší je hloubka a čím větší jsou rozměry dutiny, tím větší je amplitudový pokles registrovaný na povrchu. Tato metodika byla ověřena na známých dutinách v Brně a pokusně se zjišťovaly neznámé podzemní dutiny v Klatovech (J. Bernat 1968, 1969, 1971).

Uhlík (1969) studoval možnosti geofyzikálních metod k průzkumu nezavalených prostor ve stařinách hnědouhelné sloje. Seismických metod se dále použilo při vyšetřování dutin ve zdivu historických budov, při sledování zasypaných šachet a částečně narušených chodeb (Hrdlička a kol. 1968—1971). Bárta (1980) provedl pokusné měření metodou lomených vln v Táboře.

V zahraničí byla použita reflexní seismika ke sledování podpovrchových dutin (Cook 1965) o rozměrech desítek až stovek metrů, nacházejících se v hloubkách 300—500 m pod povrchem (solná ložiska, atomové výbuchy). Dobré výsledky byly získány v podmínkách, kdy pod dutinou existoval výrazný odrážející horizont; vyhodnocování bylo založeno na pozorování amplitud vln odražených od dutiny a od horizontu. Využívalo se „stínu“ za dutinou.

Metody lomených vln – vějířů (varianta kruhového uspořádání geofonu) bylo použito také v archeologické prospekci při vyhledávání krypt (Frantov a Pinkevič 1966). Dobré výsledky lze očekávat, nepřevýší-li mocnost nadloží krypty několik málo metrů. Je-li prostředí stejnorodé, potom čas příchodu vlny ke geofonům i amplitudy signálu budou stejné. V případě měření nad kryptou jsou registrovány anomálie času i amplitud.

Výzkumem použití seismických metod k vyhledávání a trasování podpovrchových dutin se zabývá práce Efimova (1971). Ověřovala se metodika seismického profilování na povrchu a prozařování mezi vrty (ve skupině vrtů se střídavě vždy v jednom vrtu provádí odpal trhavin, v ostatních registrace seismických vln). Při sledování chodeb o průřezu 4—9 m2 ve vápencích, pod vrstvou čtvrtohorních usazenin o mocnosti 5—12 m se dosáhlo dobrých výsledků.

V souvislosti s výstavbou města Pécs v MLR a zjišťováním stability staveb a inženýrských děl byl řešen problém sklepů (Sabo a kol. 1976), vybudovaných ve vrstvách hlin, písku a písčitých hlin, v různém uspořádání navzájem a vzhledem k povrchu. Při geofyzikálním průzkumu bylo užito seismických metod – sledování mikroseismů, měření na stěnách (doznívání), prozařování a měření na profilech. Výsledky měření byly uspokojivé.

Staré městské kanály s obezdívkou sledoval Szybiňski (1980) profilovým měřením nad kanálem. Profily situoval pod různými úhly k ose kanálu. Pro úhly 45° se vliv kanálu neprojevil. Při úhlech 22,5° vliv kanálu zvyšuje rychlost šíření vln, při úhlu 0° se registruje lomená vlna.

Parametrická měření, v rámci metodicko-výzkumných prací, byla prováděna několika geofyzikálními metodami nad známými, pevně klenutými podzemními chodbami tereziánské pevnosti Jaroměř-Josefov (Hašek a kol. 1981). Ze seismických metod byla užita metoda vějířů a profilové měření se zdrojem vlnění (úder 8 kg kladiva) na povrchu a podzemí (strop chodby). Na základě výsledků pozorování jednotlivých geofyzikálních metod (mikrogravimetrie, magnetometrie, geoelektrika, seismika) bylo možné poměrně spolehlivě lokalizovat většinu sledovaných chodeb.

Jako příklad aplikace seismiky při vyhledávání podzemních dutin si uveďme měření v širším okolí hradu Veveří u Brna. Podle nepodložených historických údajů byly před několika stoletími budovány v okolí hradu podzemní chodby, a to zejména v okolí románsko-gotické kapličky, kterou s hradem měly spojovat. O existenci chodeb nejsou dosud známy žádné přímé důkazy, ovšem existují nepřímé náznaky, naznačující předpoklad o existenci podzemních dutin (proboření pluhu apod.). Historikové předpokládají, že z krypty pod kapličkou vychází několik chodeb.

Seismické práce byly prováděny při registraci lomených vln na 4 profilech, s 2 m vzdáleností geofonů. Pro úplnost byla také uskutečněna 3 měření při kruhovém uspořádání geofonů (poloměr 7,64 m, vzdálenost geofonů 2 m, zdroj vlnění úderem kladiva ve středu kruhu). Všechna měření byla prováděna aparaturou TRIO.

 

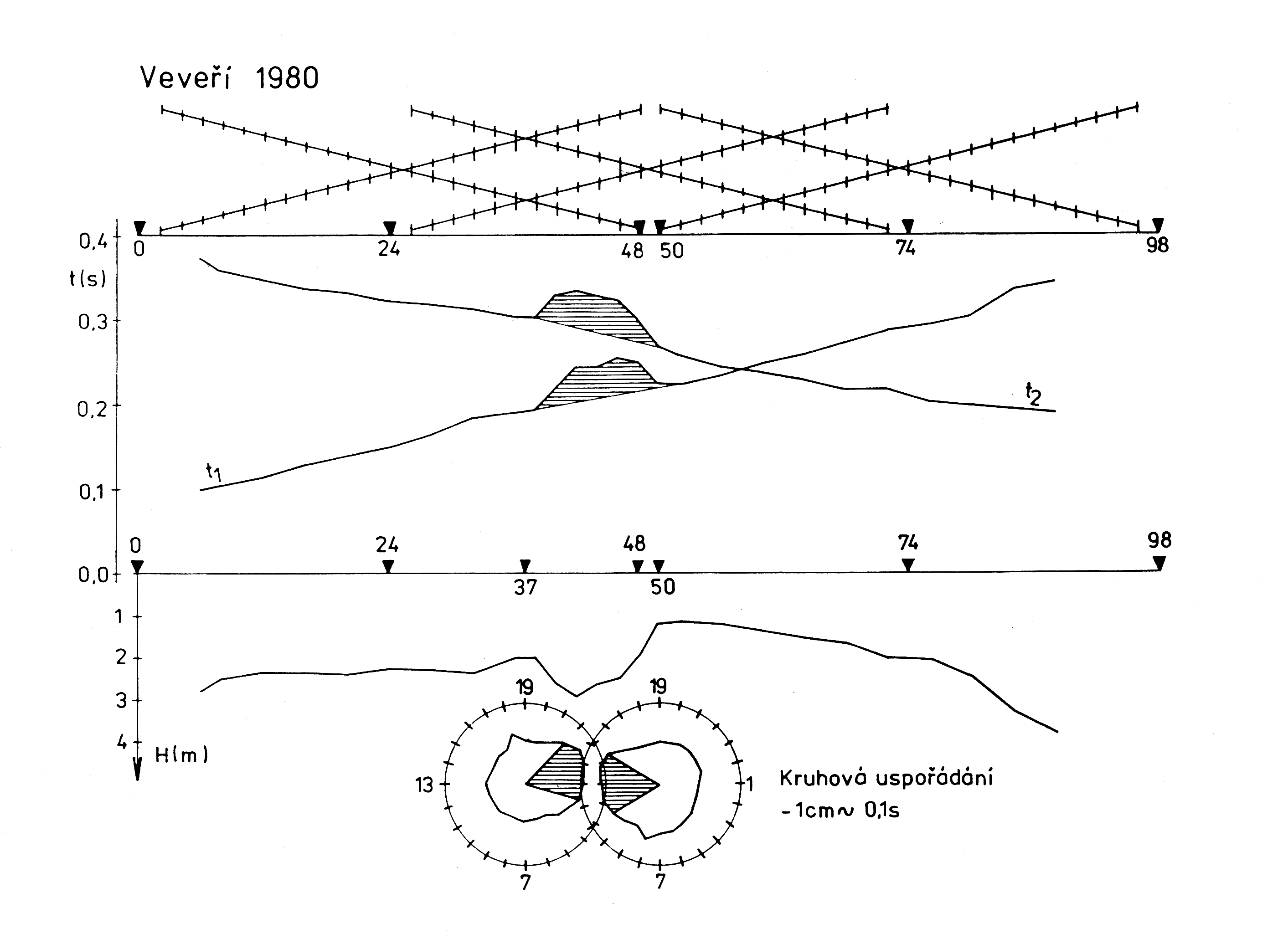
Obr.29: Ukázka výsledků seismických měření v lokalitě Veveří u Brna.

 

 

Schéma s výsledky seismických měření na jednom profilu, spolu se dvěma měřeními při kruhovém uspořádání geofonů jsou uvedeny na obr.29. V horní části obrázku je znázorněn systém měření – odpaly na staničeních 0, 24, 48, 50, 74 a 98 m a k tomu příslušné schéma rozložení geofonů (např. při odpalu 50 byly geofony rozloženy na staničeních 50—97 m). Ve spodní části jsou prezentovány výsledky měření; na dvojici tzv. vstřícných hodochron lomených vln (t1, t2) je patrná anomální oblast zvýšených časů – po přepočtu do hloubkové verze docházíme k závěru o náznaku příkopu ve střední části profilu. Tento závěr potvrzují i výsledky měření při kruhovém uspořádání geofonů (kruhy se středy na staničeních 37 a 50 m, geofony po obvodu kruhu – dosažené časy jsou znázorněny ve středních částech kruhů – 1 cm ~ 0,1 s – přičemž anomální oblasti zvýšených časů jsou vyšrafovány) a také výsledky dalších geofyzikálních disciplin – zejména vertikální elektrické sondování (VES) a odporová verze metody VDV.

Závěrem je možné konstatovat, že ve střední části uvedeného profilu by se mohlo jednat o hlubší recentní zásah nebo o zavalenou a zasypanou chodbu. Výsledky geofyzikálního měření by však bylo potřebné ověřit následným terénním výzkumem.

 


Doporučená (*) a použitá literatura: